Clausura (Grafos)

Clausura Concepto: Dícese en la Teoría de Grafos de la relación que asocia a cada nodo los vértices que pueden visitarse desde él.

Clausura. Dícese en la Teoría de Grafos de la función C(x, G) --> V* , donde G es un grafo de la forma G=<V, A>, con V conjunto de vértices y A el conjunto de aristas (o arcos, si es un dígrafo) y x es un nodo de V, un subconjunto de V o el propio G; de manera que C devuelve el conjunto V^* de todos los nodos accesibles en G desde x. C(x, G) se lee clausura de x en G .

Definición.

Sea G un grafo tal que G=<V, A>, con V conjunto de vértices y A el conjunto de aristas (o arcos, si es un dígrafo), se dice clausura o cierre de x en G a la función C(x, G) = V*, donde x es un nodo de V, un subconjunto de V o el propio G; y V^* es un subconjunto de V de todos los nodos accesibles desde x en G.

Algoritmo.

Otra definición formal de la clausura es una de tipo constructiva que conduce a la conformación del siguiente algoritmo:

1. Entradas: V, conjunto de nodos; A, conjunto de arcos del grafo; O, conjunto de vértices a clausurar.
2. C = {}
3. Mientras :
   1. Se toma un elemento x de O
   2. 
   3. 
   4. Para todo :
      1. Si entonces
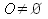4. Salida: C

Propiedades

La clausura posee una serie de propiedades que la hacen deseable para el análisis, uso y estudio en la teoría de grafos y otras ramas y especialidades.

En todos los casos siguientes se entiende que se ha definido el grafo G por el par <V,A>.

• C({}, G) = {}.
• C(G, G) = V.
• para .
• con y por extensión, con .
• Cada clausura de un grafo no orientado G son los vértices de una componente conexa completa de G.
• Para los grafos no orientados conexos G, el cierre de cualquiera de sus vértices o de un subconjunto de sus vértices, será V.

Ejemplos.

Sea el grafo G=<{Sol, Mercurio, Venus, Tierra, Luna, Marte, Fobos, Deimos}, {<Mercurio, Sol>, <Venus, Sol>, <Tierra, Sol>, <Luna, Tierra>, <Marte, Sol>, <Fobos, Marte>, <Deimos, Marte>}> con representación gráfica:

• 

Sus clausuras serían:

• C(Sol) = {Sol}
• C(Mercurio) = {Sol, Mercurio}
• C(Venus) = {Sol, Venus}
• C(Tierra) = {Sol, Tierra}
• C(Luna) = {Sol, Tierra, Luna}
• C(Marte) = {Sol, Marte}
• C(Fobos) = {Sol, Marte, Fobos}
• C(Deimos) = {Sol, Marte, Deimos}

Veáse también

• Grafo.
• Kn.

Fuentes.

1. K. Ribnikov. Análisis Combinatorio. Moscú: Editorial MIR, 1988.