Coeficiente de correlación en R
| ||||||
Correlación usando el sofware R.. Es una medida de la relación (covariación) lineal entre dos variables cuantitativas contínuas (x,y). La correlación es en esencia una medida normalizada de asociación o covariación lineal entre dos variables.
Sumario
Correlación usando el sofware R
Esta medida o índice de correlación r puede variar entre -1 y +1, ambos extremos indicando correlaciones perfectas, negativa y positiva respectivamente. Un valor de r = 0 indica que no existe relación lineal entre las dos variables. Una correlación positiva indica que ambas variables varían en el mismo sentido. Una correlación negativa significa que ambas variables varían en sentidos opuestos.
El índice de correlación r se interpreta de la siguiente manera:
- correlación despreciable: r < |0.1|
- correlación baja: |0.1| < r <= |0.3|
- correlación mediana: |0.3| < r <= |0.5|
- correlación fuerte o alta: r > |0.5|
Cálculo del coeficiente de correlación en r
La función cor() está definida en el paquete stats de la librería básica de R:
cor(x, y = NULL, use = "everything",method = c("pearson", "kendall", "spearman"))
El coeficiente de correlación τ de Kendall es no paramétrico, es decir, se puede usar cuando se viola elsupuesto de distribución normal de las variables a comparar. La correlación τ de Kendall es particularmenteadecuada cuando tenemos un set de datos pequeño con muchos valores en el mismo rango o clase. Se puedeusar por ejemplo con datos categóricos con codificación binaria (0,1). Estudios estadísticos han demostradoque el coeficiente de correlación τ de Kendall es un mejor estimador de la correlación en la población queel coeficiente de correlación no paramétrico de Spearman ρ, por lo que se recomienda usar τ para análisisde datos no paramétricos. En el argumento method se definen los coeficientes de correlación de Pearson, Kendall y Spearman.
Ejemplo: cálculo de la correlación de Pearson a partir de los datos iris definidos en el paquete datasets.
/#Cargar librerías
library("corrplot") # corrplot::corrplot()
library("psych") # psych::corr.test
library("car") # car::scatterplotMatrix
cor(iris[,1:4])
>(r<-cor(iris[,1:4]))
Sepal.LengthSepal.WidthPetal.LengthPetal.Width
Sepal.Length1.0000000 -0.1175698 0.8717538 0.8179411
Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
Petal.Length0.8717538 -0.4284401 1.0000000 0.9628654
Petal.Width0.8179411 -0.3661259 0.9628654 1.0000000
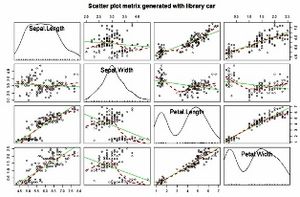
>scatterplotMatrix(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,data = iris[,1:4],main ="Scatterplotmatrixgeneratedwithlibrarycar",spread=FALSE, smoother.args=list(lty=2))#visualización de las correlaciones entre múltiples variables en matrices con el paquete car.
El coeficiente de determinación r2
El coeficiente de determinación (r2), es el coeficiente de correlación elevado al cuadrado,el cual mide lacantidad de variación en una variable que es compartida por otra. En el ejemplo anterior lacor(Petal.Length,Sepal.Length) es de0.8717538, por tanto r2 = 0.7599546. Se puede afirmar que la respuesta comparte un ~76% de la variación.
>round(r^2 * 100, 1)
Sepal.LengthSepal.WidthPetal.LengthPetal.Width
Sepal.Length 100.0 1.4 76.0 66.9
Sepal.Width 1.4 100.0 18.4 13.4
Petal.Length 76.0 18.4 100.0 92.7
Petal.Width 66.9 13.4 92.7 100.0
Cálculo de la significancia de r mediante la funcioncor.test() para dos variables
>attach(iris)
>(cor.test(Petal.Length, Sepal.Length))#significancia de correlaciónentre dos variables solamente.
Pearson'sproduct-momentcorrelation
data: Petal.Length and Sepal.Length
t = 21.646, df = 148, p-value< 2.2e-16
alternativehypothesis: true correlationisnotequal to 0
95 percentconfidenceinterval:
0.8270363 0.9055080
sampleestimates:
cor
0.8717538
Cálculo de la significancia de r mediante la funcioncorr.test() para múltiples variables
>psych::corr.test(iris[,1:4], use = "complete")#evalúa múltiples pares de variables.
Call:psych::corr.test(x = iris[, 1:4], use = "complete")
Correlationmatrix
Sepal.LengthSepal.WidthPetal.LengthPetal.Width
Sepal.Length 1.00 -0.12 0.87 0.82
Sepal.Width -0.12 1.00 -0.43 -0.37
Petal.Length 0.87 -0.43 1.00 0.96
Petal.Width 0.82 -0.37 0.96 1.00
SampleSize
[1] 150
Probabilityvalues (Entriesabovethe diagonal are adjustedformultipletests.)
Sepal.LengthSepal.WidthPetal.LengthPetal.Width
Sepal.Length 0.00 0.15 0 0
Sepal.Width 0.15 0.00 0 0
Petal.Length 0.00 0.00 0 0
Petal.Width 0.00 0.00 0 0
To seeconfidenceintervals of thecorrelations, printwiththe short=FALSE option
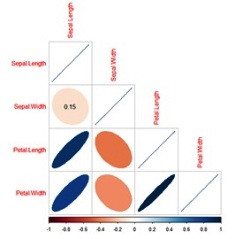
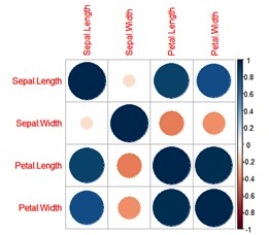
Visualización de matrices de correlación con la función corrplot()
>corrplot::corrplot(cor(iris[,1:4]))#salida por defecto de corrplot.
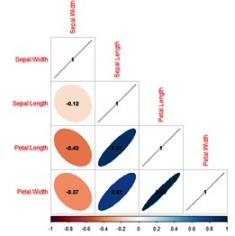
>corrplot::corrplot(cor(iris[,1:4]),method="ellipse",type="lower",order="hclust",number.cex = .9,addCoef.col = "black")
/# Añadir p-values
cor.mtest<- function(mat, conf.level = 0.95) {
mat <- as.matrix(mat)
n <- ncol(mat)
p.mat<- lowCI.mat<- uppCI.mat<- matrix(NA, n, n)
diag(p.mat) <- 0
diag(lowCI.mat) <- diag(uppCI.mat) <- 1
for (i in 1:(n - 1)) {
for (j in (i + 1):n) {
tmp<- cor.test(mat[, i], mat[, j], conf.level = conf.level)
p.mat[i, j] <- p.mat[j, i] <- tmp$p.value
lowCI.mat[i, j] <- lowCI.mat[j, i] <- tmp$conf.int[1]
uppCI.mat[i, j] <- uppCI.mat[j, i] <- tmp$conf.int[2]
}
}
return(list(p.mat, lowCI.mat, uppCI.mat))
}
> res1 <- cor.mtest(iris[,1:4], conf.level = .95)
>corrplot(cor(iris[,1:4]),method = "ellipse",type = "lower", p.mat = res11, insig = "p-value")
Fuentes
- Dougherty J, Kahavi R y Sahami M. Supervised and unsupervised discretization of continuous features. En Machine Learning: Proceedings of the Twelth International Conference, 1995
- Cuadras, C. M. (1981). Métodos de Análisis Multivariante. Eunibar. D.L. XII: 642
- Fawcett, T. (2003) ROC Graphs: Notes and Practical Considerations for Data Mining Researchers, Hewlett-Packard Company.
- Gower JC (1971) A general coefficient of similarity and some of its properties. Biometrics 27:857-871
- Johnson, D. E. (2000). Métodos Multivariados aplicados al análisis de datos. S.A. International Thomson Editores.
- Kohavi, R., and Provost, F. (1998), Glossary of Terms, Editorial for the Special Issue on Applications of Machine Learning and the Knowledge Discovery Process, Vol 30, No 2/3, Feb/March 1998.
- Maimon, O. and Rokach,L. (2005) Data Mining and Knowledge Discovery Handbook, Springer US, 2005.
- Podani J, Schmera D (2006) On dendrogram-based measures of functional diversity. Oikos 115:179-185
- Provost, F. and Fawcett, T. (2001). Robust classification for imprecise environments, Machine Learning 42: 203–231.
- R Core Team. 2017. R: A Language and Environment for Statistical Computing. Vienna, Austria: RFoundation for Statistical Computing. https://www.R-project.org/.
- Smith L, A Tutorial on Components Analysis, Tech. report, Universidad de Otago (Nueva Zelanda), 2002
- Sneath, P. H. A. y R. R. Sokal (1973). Numerical taxonomy. The principles and practice of numerical classification. San Francisco, California, EE.UU., W. H. Freeman and Co.
- Sokal, R. R. y P. H. A. Sneath (1963). Principies of numerical taxonomy. San Francisco y Londres, Freeman and Cía.
- Weiss, G. M., and Provost, F. (2003) Learning When Training Data are Costly: The Effect of Class Distribution on Tree Induction, JAIR 19, 315–354