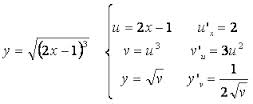Derivación de funciones compuestas
| ||||
Derivación de funciones compuestas. Para derivar funciones compuestas en una sola variablea se utliza la regla de la cadena, en el caso de funciones de más de una variable la regla de la cadena tiene varias versiones que dan la regla de diferenciación de la composición de funciones para diferentes casos.
Primer caso
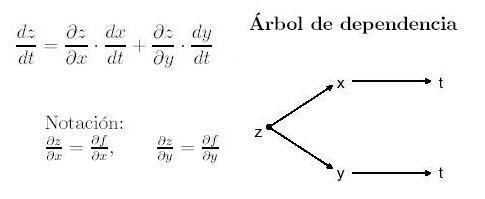
Si z= f(x,y) es una función diferenciable de los argumentos x e y, que son a su vez funciones diferenciables de una variable independiente t
x = ð(t), y = φ(t)
La derivada de la función compuesta z = f[ð(t),φ(t)] se puede calcular por la fórmula:
Ejemplo 1
Si z = f (x, y) = x2 y − y4 x3 , donde x = t3 e y = ln t, la diferencial de z respecto de t será:
d͡z/d͡x = (2xy − 3y4x2) Derivando la función z con respecto a x
d͡z/d͡y = (x2 − 4y3 x3) Derivando la función z con respecto a y
dx/dt = 3t2 Derivando x = t3
dy/dt = 1/t Derivando y = ln t
Luego sustituyendo en la fórmula resulta
d͡z/d͡t = (2xy − 3y4x2)3t2 + (x2 − 4y3 x3)1/t
sustituyendo los valores de x e y como función de t :
d͡z/d͡t = (2t3ln t - 3(ln t)4t6)3t2 + (t6 − 4(ln t)3t9)1/t
d͡z/d͡t = 6t5 ln t + t5 − 4 (ln t)3 t8 − 9(ln t)4 t8
Segundo caso
Si z es una función compuesta de varias variables independientes, por ejemplo, z = f(x,y) donde x = ð(s,t) e y = φ(s,t) s y t son variables independientes, f, ð y φ son funciones diferenciables, las derivadas parciales de z con respecto a s y t se expresan así:
Ejemplo 1
Si z = f (x, y) = x2 y − y 4 x3 donde x = t3 + 2s e y = s ln t, entonces las derivadas parciales de z respecto de s y t son:
d͡z/d͡s = (2xy − 3y4x2) 2 + (x2 − 4y3 x3)ln t
d͡z/d͡t= (2xy − 3y4x2)3t2 + (x2 − 4y3 x3)s/t
sustituyendo los valores de x = t3 + 2s e y = s ln t
d͡z/d͡s = 2 (2(t3 + 2s)sln t − (s ln t)4 (t3 + 2s)2 + ln t (t3 + 2s)2 − 4 (s ln t)3 (t3 + 2s)2</sup))
d͡z/d͡t = 3t2(2(t3 + 2s) - (s ln t)4 (t3 + 2s)2
Caso general
Si z es una función diferencial de n variables, x1 , x2 , ..., xn , donde estas a su vez son funciones diferenciables de m variables, t1 , t2 , ..., tm , entonces z es una función diferencial de t1 , t2 , ..., tm donde:
Fuente
- Cálculo. Roland Larson y otros.
- Cálculo Diferencial e Integral, Willian Granville y otros