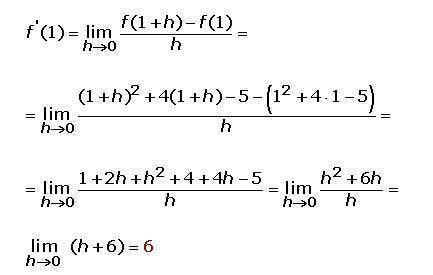Derivada de una función
| ||||
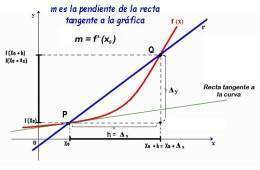
Derivada de una función. La derivada es uno de los conceptos de significado dialéctico en matemáticas. La derivada, en el caso de una función real de una variable real, es el resultado de un límite y representa, geométricamente, la pendiente de la recta tangente a la gráfica de la función en un punto. En la Física, la derivada se puede entender como la velocidad instántanea. Se puede considerar la derivada como la razón de variación de una masa poblacional respecto de la variación del tiempo.
Se considera una secante que pasa por un punto fijo de una curva y pasa por otro punto de la misma curva ( las abscisas están en un intervalo abierto del punto fijo). Consideremos la infinidad de secantes que pasan por el punto fijo y el otro punto de la secante se aproxima a él; la recta secante, en el límite si existe, se convierte en recta tangente a la curva en el punto fijo. Hay un salto cualitativo ( cambio dialéctico) de recta secante a recta tangente.
Sumario
Historia
En cálculo (rama de las matemáticas), la derivada representa cómo una función cambia (valor de la variable dependiente) a medida que su entrada (valor de la variable independiente) cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una función en un punto dado (o sea su velocidad de variación); por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo, es la velocidad instantánea con la cual el vehículo está viajando.
La derivada de una función es un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.
Derivada de una función en punto
Se llama derivada de la función y = f(x) en el punto x0 y se denota por f’(x) al límite de la razón ![]() es decir:
es decir:
Si este limite existe se dice f(x)es derivable en el punto X0.
Ejemplo
Hallar la derivada de la función f(x) = x2 + 4x − 5 en x = 1.
Interpretación Geométrica de la derivada de una función en un punto
La derivada de una función f(x) en el punto de abscisa x = a, es la pendiente de la tangente a la gráfica, que representa esa función, en el punto P (a,f(a))
Ejemplo
Determina la ecuación de la recta tangente a la gráfica de g(x)= x2 en el punto cuya abscisa es 2.
Notaciones
Las derivadas de la función y = f(x) se denotan también de otras formas:
f’(x) Para denotar la función derivada
Y’(xo) Para denotar la derivada en X0
![]() Para denotar la función derivada
Para denotar la función derivada
Puede ocurrir que la derivada de la función sea una función derivable. Por lo que a la derivada de la derivada de f se le llama segunda derivada de f y se denota f’’
Analogamente, la derivada de la segunda derivada de f es la tercera derivada de f que se denota por f’’’y así sucesivamente.
Derivadas Laterales
Una función es derivable en un punto si, y sólo si, es derivable por la izquierda y por la derecha en dicho punto y las derivadas laterales coinciden.
Ejemplo
Derivada de la función potencia exponente
(xn )' = n xn-1 , n es un número entero positivo o natural , n>=1
Ejemplo
Calcula la derivada de y = x5 en x0 = 3.
f'(x) = 5 x4
f'(3) = 5 (3)4 = 405
Proposición
Si una función f(x) es derivable en en el punto x= a, entonces la función es continua en el punto x=a.
De modo que en los puntos de discontinuidad la función no es derivable. Además que una función sea continua en un punto no garantiza necesariamente que la función sea derivable en dicho punto. Ejemplo: la función y = 1+|x-2| es continua en todo su dominio, pero no es derivable en x = 2. Que una función sea continua es condición necesaria para que una función sea derivable. [1]
Bibliografía
- Cálculo. Roland Larson y otros.
- Cálculo diferencial e integral, William Granville y otros
- Cálculo diferencial e integral, Stefan Banach
Referencias
- ↑ Piskunov N. Cálculo diferencial e integral tomo I, Editorial MIR Moscú Sexta edición ( 1983)