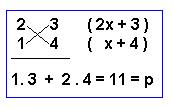Descomposición factorial
| ||||||
Descomposición factorial. Se utiliza para expresar cualquier número entero positivo como producto de potencias de números primos.
Sumario
- 1 Factores
- 2 Métodos para la factorización de polinomios
- 3 Factorizar un monomio
- 4 Factorizar un polinomio
- 5 Caso I: Factor común
- 6 Caso II. Factor común por agrupación de términos
- 7 Caso III. Trinomio cuadrado perfecto
- 8 Caso IV. Diferencia de cuadrados perfectos
- 9 Caso V. Trinomios de la forma x2 + px + q
- 10 Caso VI. Trinomios de la forma mx2 + px + q con (m ≠ 1)
- 11 Fuentes
Factores
Se llaman factores o divisores de una expresión algebraica a los que el producto entre sí (de éstos factores) nos da la expresión primitiva. Así, efectuando el producto entre a y a + b, se obtiene:
a y a+b, cuyo producto entre sí dan la expresión a2 + ab, estos son los divisores de a2 + ab de tal manera que:
(x+3)(X+5) = x2 + 8x + 15
Donde (x+3)(X+5) son los factores de x2 + 8x + 15
Métodos para la factorización de polinomios
Todo Polinomio se puede factorizar utilizando números reales, si se consideran los números complejos. Existen métodos de factorización, para algunos casos especiales.
Binomios
Trinomios
- Trinomio cuadrado perfecto
- Trinomio de la forma x²+bx+c
- Trinomio de la forma ax²+bx+c
Polinomios
- Factor común
Factorizar un monomio
Se descompone el término en el producto de factores primos.
Ejemplo:
Factorizar un polinomio
No todo polinomio se puede descomponer en un producto indicado de dos o más factores distintos de 1, ya que de la misma forma que en Aritmética, hay números primos que sólo son divisibles por la unidad y por sí mismos, en Algebra, hay expresiones algebraicas que sólo son divisibles por la unidad y por ellas mismas, en consecuencia, no son el producto de otras expresiones algebraicas. Así a + b no puede descomponerse en dos factores distintos de 1 porque sólo es divisible por a + b y por la unidad.
A continuación diferentes casos de descomposición factorial.
Caso I: Factor común
Factor común.
Cuando todos los términos de un polinomio tienen un factor común.
Ejemplos:
a) Descomponer en factores a2 + 2a
a2 y 2a contienen el factor común a. Se escribe este factor común como coeficiente de un paréntesis, dentro de este paréntesis se escriben los cocientes obtenidos de efectuar el cociente entre a2 y a y 2a y a
Obteniendo como resultado: a2 + 2a = a(a + 2)
b) Factorizar 10b - 40ab2
Los coeficientes numéricos tienen los factores 2,5 y 10. Se toma el 10 porque siempre se escoge el mayor factor común. De las variables, el único factor común es b ya que se haya en los dos términos del binomio y se toma con su menor exponente. El factor común será 10b
Obteniendo: 10b - 40ab2 = 10b(1 - 4ab)
c) Descomponer en factores:
10a2 - 5a + 15a3 = 5a(2a - 1 + 3a2)
Factor común de un polinomio
a) Descomponer en factores: x(a+b)+y(a+b)
Los dos términos de la expresión tienen como factor común (a+b). Se escribe (a+b) como coeficiente de un paréntesis, dentro del paréntesis se escriben los cocientes de dividir x(a+b) entre (a+b) y y(a+b) entre (a+b).
Factorizando se obtiene:
x(a+b)+y(a+b) = (a+b)(x+y)
x(a+b)+y(a+b) = ax+bx+ay+yb y (a+b)(x+y) = ax+ay+bx+by
Obteniendo:
x(a+b)+y(a+b) = (a+b)(x+y) y ax+bx+ay+yb = ax+ay+bx+by
Caso II. Factor común por agrupación de términos
Se agrupan los términos que tengan factor común, asociándolos entre paréntesis y luego se extrae el factor común de cada uno.
Ejemplos
a) Factorizar ax + by +ay + by
Los dos primeros términos tienen el factor común x, y los dos últimos tienen el factor común y, asociando los dos primeros términos en un paréntesis y los dos últimos también en un paréntesis precedido de un signo + ya que el tercer término es positivo se obtiene:
ax+bx+ay+by = (ax+bx)(ay+by)
ax+bx+ay+by = x(a+b) + y(a+b) extrayendo los factores comunes
ax+bx+ay+by = (a+b)(x+y) factorizando
Nota: La asociación de términos puede hacerse de varios modos y siempre se obtendrá el mismo resultado.
Caso III. Trinomio cuadrado perfecto
Una cantidad es cuadrado perfecto cuando es el producto de dos factores iguales.
Asi, 16a2 es cuadrado perfecto de 4a.
En efecto (4a2) = 4a x 4a = 16a2, 4a cantidad que multiplicada por si misma da 16a2, 4a es la raíz cuadrada de 16a2.
Sin embargo (-4a2) = (-4a)((-4a) = 16a2, luego (-4a) es también raíz de 16a2, por lo que la raiz cuadrada de una cantidad positiva tiene los signos (+) y (-).
Raíz cuadrada de un monomio
Para extraer la raíz cuadrada de un monomio, se saca la raíz cuadrada de su coeficiente numérico y se dividen los exponentes de cada cantidad literal entre 2.
Ejemplo: La raíz cuadrada de 25a2b4 es 5ab2
Un trinomio es cuadrado perfecto cuando es el cuadrado de un binomio, es decir, es el producto de dos binomios iguales.
Así, a2 + 2ab + b2 es cuadrado perfecto porque es el cuadrado de a + b
Por tanto:
(a + b)2 = (a + b)(a + b) = a2 + 2ab + b2
Regla para identificar si un trinomio es cuadrado perfecto
Un trinomio ordenado con relación a una letra es cuadrado perfecto cuando el primer y tercer término son cuadrados perfectos (o tienen la raíz cuadrada exacta) y positivos, y el segundo término equivale al doble del producto de éstas raíces cuadradas.
Ejemplo:
a) a2 - 4ab + 4b2 es cuadrado perfecto porque:
Raíz cuadrada de a2 = a
Raíz cuadrada de 4b2 = 2b
Doble producto de estas raíces 2 x a x 2b = 4ab
Regla para factorizar un Trinomio Cuadrado Perfecto
Se extrae la raíz cuadrada del primer y tercer término del trinomio y se separan estas raíces por el signo del segundo término. El binomio ya formado, que es la raíz cuadrada del trinomio, se multiplica por sí mismo o se eleva al cuadrado.
Ejemplo:
a) El trinomio a2 + 8ab + 16b2 es cuadrado perfecto ya que:
raíz cuadrada de a2 = a raíz cuadrada de 16b2 = 4b
Doble producto de las raíces: 2 x a x 4b = 8ab
Caso IV. Diferencia de cuadrados perfectos
En los productos notables se halla el producto suma por diferencia, es decir, el producto entre la suma de dos binomios y su diferencia equivale a una diferencia de cuadrados perfectos.
Regla para factorizar una diferencia de cuadrados
Se extrae la raíz cuadrada al minuendo y al sustraendo y se efectúa el producto entre la suma de éstas raíces cuadradas y su diferencia.
Ejemplificando:
Factorizar
a) x2 - 9 =(x-3)(x+3)
raíz del primer témino: x
raíz del segundo término: 3
Doble producto de la suma por la diferencia: (x-3)(x+3) = x2 - 9
b) 16x2 - 25y4
raíz del primer término: 4x
raíz del segundo término: 5yx2
Solución: (4x - 5y2)(4x + 5y2)
c) (a + b)2 - c2
raíz del primer término: (a + b)
raíz del segundo término: c
Solución: [(a + b) - c][(a + b) + c]
Caso V. Trinomios de la forma x2 + px + q
En el producto notable (x + a)(x + b) = x2 + (a + b)x + ab observa que se obtiene un trinomio de la forma x2 + px + q, haciendo para ello a + b = p y ab = q
Por tanto:
Un trinomio de la forma x2 + px + q se puede descomponer en el producto de dos factores: (x + a) y (x + b) si podemos encontrar dos números a y b cuya suma algebraica sea p y cuyo producto sea q
Regla práctica para factorizar el trinomio
1) El trinomio se descompone en dos factores binomios, cuyo primer término es x, es decir, la raíz cuadrada del primer término del trinomio.
2) En el primer factor, después de x se escribe el signo del segundo término del trinomio, y en el segundo factor, después de x se escribe el signo que resulta de multiplicar el signo del 2do término del trinomio y el signo del tercer término del trinomio.
3) Si los dos factores binomios tienen en el medio signos iguales se buscan dos números cuya suma sea el valor absoluto del segundo término del trinomio y cuyo producto sea el valor absoluto del tercer término del trinomio. Estos números son los segundos términos de los binomios.
4) Si los dos factores binomios tienen en el medio signos distintos se buscan dos números cuya diferencia sea el valor absoluto del segundo término del trinomio y cuyo producto sea el valor absoluto del tercer término del trinomio. El mayor de estos números es el primer término del primer binomio, y el menor, es el segundo término del segundo binomio.
Ejemplos:
Descomponer en factores:
a) x2 + 9x + 20 = (x + 4)(x + 5), pues 4 + 5 = 9 y 4 x 5 = 20
b) a2 - 8a + 12 = (a - 6)(a - 2), pues (-6) + (-2) = (-8) y (-6)(-2) = 12
c) b2 + 3b - 28 = (b - 4)(b + 7), pues (-4) + 7 = 3 y (-4) x 7 = -28
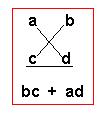
Caso VI. Trinomios de la forma mx2 + px + q con (m ≠ 1)
Observemos que el producto:
(ax + b)(cx + d) = acx2 + adx + bcx + db
= acx2 + (ad + bc)x + db, es de la forma mx2 + px + q (haciendo m = ac, p = ad + bc y q = bd).
Luego, siempre que sea posible hallar a, b, c, d, será posible factorizar
¿Cómo determinar estos números?
a) Se selecciona una descomposición factorial de m y otra de q:
m = ac y q = bd
b) Se calculan los productos cruzados ad y bc, y se adicionan estos productos:
c) Si bc + ad = p, entonces los factores del trinomio dado son (ax+b) y (cx+d). En caso contrario se ensaya con otra combinación de factores para m y para q
Ejemplos:
a) 2x2 +11x + 12 m = 2 = 2 x 1 q = 12 = 3 x 4
luego 2x2 +11x + 12 = (2x + 3)(x + 4)
Si no se obtiene el coeficiente p, entonces se ensaya con otras factorizaciones.
Por ejemplo: 2 = 1 · 2, 12 = 6 · 2, 12 = 1 · 12, 12 = 4 · 3, 12 = 2 · 6
También puede que ambos factores sean negativos, pues el resultado es positivo:
2 = (-1) · (-2) , 12 = (-6) · (-2)
Fuentes
- Artículo Descomposición factorial. Disponible en ¨maralboran.org¨. Consultado el 16 de julio del 2011.
- Artículo Polinomios. Disponible en ¨usuarios.multimania.es¨. Consultado el 16 de julio del 2011.
- Artículo Factorización. Disponible en ¨maralboran.org¨. Consultado el 16 de julio del 2011.