Distancia entre dos puntos
| ||||||
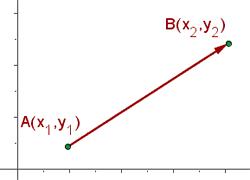
Distancia entre dos puntos.Dados dos puntos cualesquiera A(x1,y1), B(x2,y2), definimos la distancia entre ellos, d(A,B), como la longitud del segmento que los separa.
Historia
Geometría analítica, rama de la Geometría en la que las líneas rectas, las curvas y las figuras geométricas se representan mediante Expresiones algebraicas y numéricas usando un conjunto de ejes y coordenadas. Cualquier punto del Plano se puede localizar con respecto a un par de ejes Perpendiculares dando las distancias del punto a cada uno de los ejes.
Uno los filósofos más notables que contribuyó al desarrollo de las Matemáticas fue [René Descartes]] pues realizó la sistematización de la Geometría Analítica. Fue el primer matemático que intentó clasificar las curvas conforme al tipo de ecuaciones que las producen y contribuyó también a la elaboración de la teoría de las ecuaciones.
Nacido el 31 de marzo de 1596 en La Haye, hoy Descartes, era hijo de un miembro de la baja nobleza y perte- necía a una familia que había dado algu-nos hombres doctos.
En 1649 fue invitado a acudir a Estocolmo para impartir clases de filosofía a la reina Cristina de Suecia. Falleció, en la capital sueca, el 11 de febrero de 1650.
Distancia entre dos puntos
El Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.
Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1).
Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. (y1 - y2)
Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Demostración
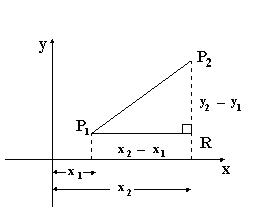
Sean P1 (x1, y1) y P2 (x2, y2) dos puntos en el plano.
La distancia entre los puntos P1 y P2 denotada por d =esta dada por:
Ejemplos
- Calcular la distancia entre los puntos: A(2, 1) y B(-3, 2).