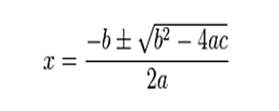Ecuación de segundo grado

Ecuación de Segundo Grado Concepto: Toda ecuación de la forma ax2 + bx + c = 0 (a ≠ 0)

Ecuación de segundo grado. Toda ecuación de la forma ax² + bx + c = 0 (siendo a ≠ 0) se denomina ecuación de segundo grado o cuadrática. La ecuación es completa si los tres coeficientes (a, b y c) son distintos de cero. Si algunos de los coeficientes b y c es igual a 0, entonces la ecuación es incompleta .

Resolución

Existen varias técnicas o métodos para calcular las raíces (soluciones) de una ecuación de segundo grado. La técnica más empleada es la aplicación de la fórmula cuadrática.

Fórmula cuadrática

Las soluciones de una ecuación de segundo grado en la forma general ax² + bx + c = 0 vienen dadas por la fórmula cuadrática:

Al radicando de fórmula, D = b² - 4·a·c, se le denomina discriminante de la ecuación. El número (y tipo) de soluciones queda determinado por el signo del discriminante.

Tipos de soluciones

Las ecuaciones de segundo grado tienen siempre dos soluciones complejas (que a su vez pueden ser reales). En el caso de la ecuación con coeficientes reales, pueden darse las siguientes tres situaciones

Una solución

Si el discriminante es 0, D = 0, entonces las dos soluciones son reales e iguales, por lo que puede decirse que existe una única solución (de multiplicidad doble).

Ejemplos:

• La ecuación x² + 2x + 1 = 0 tiene una única solución x = -1.
• La ecuación x² -2x +1 = 0 tiene una única solución x = 1.

Dos soluciones (reales)

Si el discriminante es positivo, D > 0, entonces existen dos soluciones reales distintas (de multiplicidad 1).

Ejemplos:

• La ecuación incompleta x² - 1 = 0 tiene dos soluciones reales: x=1 y x = -1. Su discriminante es D = 4 > 0.
• La ecuación completa x² + x - 2 = 0 tiene dos soluciones reales: x=1 y x = -2. Su discriminante es D = 9 > 0.

Dos soluciones no reales

Si el discriminante es negativo, D < 0, entonces las dos soluciones son números complejos conjugados. Esto se debe al hecho de que la raíz cuadrada de un número negativo es un número complejo. Es común decir que la ecuación no tiene soluciones, refiriéndose a que la ecuación no tiene soluciones reales. En el caso de que los coeficientes sean números complejos, existen exactamente dos raíces complejas no conjugadas (habrá que hallar raíz de un número complejo).

Ejemplos:

• La ecuación incompleta x² + 1 = 0 tiene dos soluciones complejas: x = i y x = -i. Su discriminante es D = -4 < 0.
• La ecuación completa x² - 2x + 5 = 0 tiene dos soluciones complejas: x = 1 + 2i y x = 1- 2i. Su discriminante es D = -16 < 0.

Ecuaciones incompletas

Las ecuaciones de segundo grado son incompletas si b = 0 ó c = 0. Se pueden resolver estas ecuaciones sin necesidad de la fórmula cuadrática:

• Si b = 0, entonces la ecuación es ax² + c = 0. Por tanto, x² = -c/a. Tomando raíces, las soluciones son x = ± √(-c/a).
• Si c = 0, entonces la ecuación es ax² + bx = 0. Factorizando, la ecuación es equivalente a la ecuación x(ax+b) = 0. Al escribirla de este modo, se deduce que una solución es x = 0 y la otra es x = -b/a.
• Si b = c = 0, entonces la ecuación es ax² = 0. Esta ecuación tiene la única solución x = 0 (de multiplicidad doble).

Propiedades teóricas

Algunas propiedades teóricas de las ecuaciones de segundo grado son:

• Suma y producto de las soluciones: si S y P son la suma y el producto, respectivamente, de las soluciones de la ecuación ax² + bx + c = 0, entonces S = -b/a y P = c/a.
• Soluciones complejas: si el número complejo z es una solución de una ecuación de segundo grado con coeficientes reales, entonces su conjugado es la otra solución de dicha ecuación.
• Ecuación obtenida a partir de la suma y del producto de sus soluciones: una ecuación de segundo grado cuyas soluciones son a y b es x² + (a+b)x + a·b = 0

• Factorización de una ecuación: si x₁ y x₂ son las soluciones de la ecuación ax² + bx + c = 0, entonces la ecuación puede escribirse de forma factorizada como a(x - x₁)(x - x₂) = 0. De hecho, ax² + bx + c = a(x - x₁)(x - x₂).

Véase también

• Ecuación
• Parábola
• Ecuación Bicuadrada