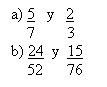Mínimo común múltiplo
| ||||||
La búsqueda del mínimo común múltiplo es un procedimiento matemático que permite resolver problemas prácticos.
Por ejemplo: Se ha organizado en el colegio un campeonato de fútbol y otro de voleibol, de manera que se celebra un partido de fútbol cada 3 días y uno de voleibol cada 4 días. Si hoy se ha celebrado un partido de ambos deportes, ¿dentro de cuántos días volverán a coincidir?
Sumario
Mínimo común múltiplo
Mínimo común múltiplo, de dos o más números naturales, es el menor número que los contengan un número exacto de veces a todos ellos, exceptuando el cero.
Es el más pequeño de los múltiplos comunes de varios números, exceptuando el cero.
Es el menor múltiplo común distinto de cero.
Ejemplo: El mínimo común múltiplo de 6, 8 y 12 es 24, porque este es el número más pequeño que los contiene exactamente.
El mínimo común múltiplo de varios números (por ejemplo: a, b, c) se expresa abreviadamente por:
m. c. m. (a, b, c) o bien MCM (a, b, c)
Para obtener el mínimo común múltiplo de varios números naturales, existen varios métodos:
Métodos para hallar el MCM
1. Por inspección
Se ve sucesivamente si el mayor de esos números, o su doble, o su triple, etc., es múltiplo de los otros números dados. El primero que lo sea es el MCM de todos ellos.
Ejemplos:
- Hallar el MCM de 2, 5 y 10: probamos el mayor, 10, y como es múltiplo de los otros dos, 10 es el MCM de 2, 5 y 10.
- Hallar el MCM de 12, 15, y 20: el mayor es 20, que no es múltiplo de los otros dos, probamos su doble, 40, que tampoco lo es, y su triple, 60, y como este sí es múltiplo de los otros dos, 60 es el MCM de 12, 15 y 20.
- Hallar el MCD de 5, 8 y 10: Probamos el 10, su duplo, 20, su triplo, 30, su cuádruplo, 40, y como este es el primero que es múltiplo de los otros dos, este es el MCM de los números dados.
En este método las operaciones son sencillas y se hacen mentalmente por lo que se sugiere cuando se trata de números pequeños.
2. Por números primos. Descomposición en factores
Se descomponen los números dados en factores primos. Para formar el MCM se toman todos los factores distintos, comunes o no, con el mayor exponente que presenten en las descomposiciones de los números dados. El producto de esos factores será el MCM de los números dados.
Este método es el mejor siempre que no haya grandes dificultades para descomponer los números dados en sus factores primos.
Ejemplo 1: Hallar el MCD de 180, 240 y 1400:
Descomponemos los números en factores primos.
Expresamos los números como productos, si algunos de los factores se repiten lo escribimos como potencia.
180 = 22 x 32 x 5
240 = 24 x 3 x 5
1400 = 23 x 52 x 7
Tomamos todos los factores distintos que aparecen en las descomposiciones de estos números sean comunes o no. Dichos factores son. 2, 3, 5 y 7. A cada uno le ponemos un exponente igual al mayor que tenga en cualquiera de las descomposiciones de los números dados, en este caso sería 24, 32, 52 y 7
Luego: MCM (180, 240, 1400) = 24 x 32 x 52 x 7 = 25 200
Respuesta: El MCM (180, 240, 1400) = 25 200.
Ejemplo 2: Hallar el MCM de 442, 884 y 962:
Prescindiendo de 442, por ser divisor de 884, resulta
- 884 = 22·13·17
- 962= 2·13·37
MCM(442,884, 962) = 22·13·17·37=32708
3. Por divisiones sucesivas. (Hay que distinguir dos casos)
Si se trata de dos números: se halla el MCD de los dos, se divide uno de ellos por ese MCD y el cociente se multiplica por el otro. El producto que se obtenga será el MCM de los dos números dados.
Ejemplos:
- Hallar el MCD de 180 y 240: Primero hallamos el MCD de esos 2 números por el método que desees). El MCD(180,240) es 60. Y ahora hallamos el MCM: MCM (180, 240) = 180 / 60 · 240 = 720.
- Hallar el MCM de 180, 240 y 1400: Es conveniente empezar por los dos mayores. Primero buscamos el MCD(1400,240)=40. Y ahora hallamos el MCM(1400, 240) = 240 / 40 · 1400 = 6 x 1400 = 8400. Buscamos del mismo modo, el MCM de ese MCM, 8400 y del otro número dado. El MCD(8400, 180) = 60, entonces el MCM (8400, 180) = 180 / 60 · 8400 = 3 · 8400 = 25200.
Resumen:
Debe recordarse que:
1-Si se trata de hallar el MCM de dos números y uno de ellos es múltiplo del otro, el primero, el múltiplo, es el MCM de los dos números dados.
2- No debe considerarse como primo un número hasta que no se haya hecho la investigación necesaria.
3- Al hallar el MCM por el método del MCD, este debe buscarse por divisiones sucesivas.
4- El MCM de varios números primos es igual a su producto.
Regla general para hallar el MCM de varios números.
1- Se observa si alguno de los números dados es múltiplo de otro. En este caso se prescinde del divisor..
2- Se elige cuál de los métodos se va a emplear de acuerdo con lo siguiente:
• Si los número son pequeños: método de inspección
• Si lo números son grandes, pero la descomposición en factores es fácil: método de descomposición en factores
• Si lo números son grandes, pero la descomposición en factores es difícil: método de divisiones sucesivas.
Aplicaciones del MCM
1. Reducir fracciones a común denominador.
Ejemplo: Reducir a común denominador las siguientes fracciones:
- cinco doceavos (5/12)
- siete novenos (7/9)
- cinco dieciochoavos (5/18)
Factorizamos los denominadores:
- 12 = 22 • 3
- 9 = 32
- 18 = 2 • 32
Escogemos los factores primos comunes y no comunes, elevados al mayor exponente. El MCM (12, 9, 18) = 22 • 32 = 4 • 9 = 36. Ya tenemos el nuevo denominador.
Ahora tan solo nos queda calcular tres fracciones equivalentes a las originales pero que tengan por denominador 36. Para ello, dividimos 36 entre 12, 9 y 18 y sabemos por cuánto tenemos que multiplicar los numeradores antiguos para obtener los nuevos: 36: 12 = 3; por lo que multiplicamos 5 x 3 = 15; 36: 9 = 4 y multiplicamos 7 x 4 =28; 36: 18 = 2 y multiplicamos 5 x 2 = 10.
Resumiendo: el denominador común de las tres fracciones es 36 y los nuevos numeradores son 15, 28 y 10, respectivamente. Así que las fracciones anteriores reducidas a común denominador quedarían de esta forma:
- quince treinta y seisavos (15/36)
- veintiocho treinta y seisavos (16/36)
- diez treinta y seisavos (10/36)
2. Resolver problemas de la vida práctica.
Ejemplo: Estoy en la playa por la noche y veo dos faros en la costa. Observo que el destello de luz de uno de ellos ocurre cada 8 segundos. En cambio, la luz del otro faro aparece cada 12 segundos. ¿Habrá algún momento en el que pueda ver el destello de ambos faros a la vez? Si es así, ¿cada cuántos segundos coincidirán los dos?
Solución: Buscamos una cantidad de segundos que sea múltiplo de 8 y de 12 y que a la vez sea el más cercano. Es decir, estamos buscando el MCM (8, 12).
Factorizamos 8 y 12:
8 = 23
12 = 22 x 3
Escogemos los factores primos comunes y no comunes, elevados al mayor exponente, y calculamos el mínimo común múltiplo.
MCM (8, 12) = 23 • 3 = 8 • 3 = 24.
Por lo tanto, comprobamos que las luces de los dos faros se verán al mismo tiempo cada 24 segundos.
Ejercicios para repasar
1. Halla el mínimo común múltiplo de las siguientes series de números.
a) 32 y 68
b) 84 y 95
c) 140, 325 y 490
d) 725, 980 y 1.400
2. Reduce a común denominador las siguientes fracciones.
3. Estoy en la parada del autobús y observo que los autobuses de la línea roja pasan cada 4 minutos, y que los amarillos paran cada 6 minutos. Uno de los conductores me ha dicho que cada 12 minutos coinciden en la parada un autobús rojo y otro amarillo. ¿Cómo lo puede saber?
4. Se ha organizado en el colegio un campeonato de fútbol y otro de voleibol, de manera que se celebra un partido de fútbol cada 3 días y uno de voleibol cada 4 días. Si hoy se ha celebrado un partido de ambos deportes, ¿dentro de cuántos días volverán a coincidir?
5. Determinar la menor cantidad de kilogramos de un producto que se pueda pesar en una balanza utilizando diferentes pesas.
6. Un viajante va a Sevilla cada 18 días, otro va a Sevilla cada 15 días y un tercero va a Sevilla cada 8 días. Hoy día 10 de enero han coincidido en Sevilla los tres viajantes. ¿Dentro de cuántos días como mínimo volverán a coincidir en Sevilla?
7. Andrés tiene en su tienda los botones metidos en bolsas. En la caja A tiene bolsitas de 24 botones cada una y no sobra ningún botón. En la caja B tiene bolsitas de 20 botones cada una y tampoco sobra ningún botón. El número de botones que hay en la caja A es igual que el que hay en la caja B. ¿Cuántos botones como mínimo hay en cada caja?
8. Teresa tiene un reloj que da una señal cada 60 minutos, otro reloj que da una señal cada 150 minutos y un tercero que da una señal cada 360 minutos. A las 9 de la mañana los tres relojes han coincidido en dar la señal. ¿Cuántas horas, como mínimo, han de pasar para que vuelvan a coincidir? ¿A qué hora volverán a dar la señal otra vez juntos?
9. Rosa tiene cubos azules de 55 mm de arista y cubos rojos de 45 mm de arista. Apilando los cubos en dos columnas, una de cubos azules y otra de cubos rojos, quiere conseguir que las dos columnas sean iguales. ¿Cuántos cubos, como mínimo, necesita de cada color?
Fuentes
- Mínimo común múltiplo: método y test (Matesfacil.com)
- Mínimo común múltiplo (Wikipedia.org)
- Sócrates Rosell Franco. Aritmética. Volumen I. Segunda Edición.
- Microsoft Encarta. Múltiplo de un número. El máximo común divisos de varios números.
- Libro de texto Secundaria Básica. 9no Grado.
- Múltiplos y divisores.