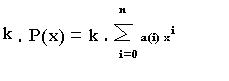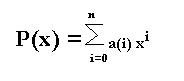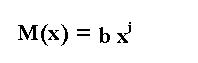Multiplicación de polinomios
| ||||||
Multiplicación de polinomios. Se deben multiplicar todos los monomios de unos, por todos los del otro y sumar los resultados.
Sumario
Definición de polinomio
Un polinomio es una expresión algebraica que se obtiene al expresar cualquier suma de monomios no semejantes.
Grado de un polinomio
- Es el grado del término de mayor grado.
- El término de primer grado se llama término lineal.
- El término de grado cero se denomina término independiente.
Valor numérico de un polinomio
Para hallar el valor numérico de un polinomio se sustituyen las indeterminadas por sus valores y se efectúan las operaciones indicadas.
Multiplicación de un número por un polinomio
Sea P(x) un polinomio , el producto de este polinomio por un escalar k, es un polinomio k P(x), en el cual cada uno de los coeficientes de los del polinomio se ha multiplicado por k. Si el polinomio es:
Multiplicando por k:
Se obtiene:
Ejemplo:
P(x) = 4x4 + 7 x5 – 6x6
Multiplicar por 8
P(x) = 8 . (4x4 + 7 x5 – 6 x6)
Obteniendo como resultado
8. P(x) = 32 x4 + 56 x5 – 48 x6
Multiplicación de un polinomio por un monomio
Sea P(x) un polinomio , y M(x) un monomio, el producto P(x)*M(x) es un polinomio que resulta de multiplicar los coeficientes del polinomio por los del monomio, y sumar a los grados del polinomio el del monomio, si el polinomio es:
y el monomio es:
el producto del polinomio por el monomio será:
Agrupar los términos:
El producto de exponentes de la misma base, es la base elevada a la suma de los exponentes:
Ejemplo:
3x2 · (2x3 − 3x2 + 4x − 2)
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
3x2 · (2x3 − 3x2 + 4x − 2)= 6x5− 9x4 + 12x3 − 6x2)
Multiplicación de dos polinomios
Dados dos polinomios P(x) de grado n y Q(x) de grado m, el producto de estos dos polinomios P(x) * Q(x) que será un polinomio de grado n + m, así si:
Se obtiene:
Al aplicar las propiedades correspondientes se obtiene:
Ejemplo:
P(x) = 2x2 − 3
Q(x) = 2x3 − 3x2 + 4x
Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.
P(x) · Q(x) = (2x2 − 3) · (2x3 − 3x2 + 4x) = 4x5 − 6x4 + 8x3 − 6x3 + 9x2 − 12x
Se suman los monomios del mismo grado.
= 4x5 − 6x4 + 2x3 + 9x2 − 12x
Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
También se pueden multiplicar polinomios de siguiente modo:
Fuentes
- Artículo Polinomios. Disponible en ¨www.vitutor.com¨
- Artículo Multiplicación de polinomios. Disponible en ¨es.wikipedia.org¨
- Artículo Multiplicación. Disponible en ¨www.slideshare.net¨