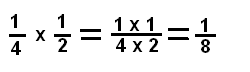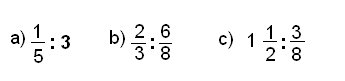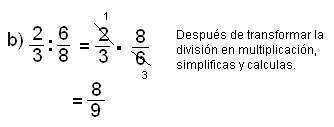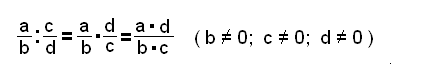Multiplicación y división de fracciones comunes
La multiplicación y división de fracciones comunes. Muy utilizadas en la vida práctica ante situaciones dadas generalmente para compartir y / o repartir algo.
Sumario
Reseña histórica
La teoría y el cálculo de las fracciones como la utilizamos en la actualidad, se le atribuye al matemático hindú Brahmagupta (600 años a.n.e.). Gracias a los matemáticos indios, que revolucionaron el arte de calcular, podemos ahora expresar y calcular con fracciones de una forma más simple.
Ejemplo graficable
Si Jaime en una hora recorre 8/3 de milla, ¿cuánto recorre en media hora? La respuesta es sencilla: la mitad de la distancia propuesta, esto es 8/3x1/2 = 8x1/3x2 = 4/3 de milla.
Multiplicación de fracciones comunes
Al igual que los números naturales, las fracciones se pueden multiplicar.
Por ejemplo:
Si quieres saber el tiempo que inviertes en practicar la ortografía dedicando ¼ (un cuarto) de hora 3 veces a la semana, ¿cómo lo planteas?.
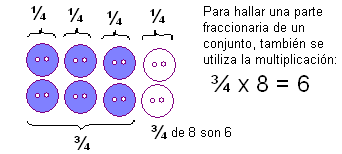
¿Necesitas conocer cuántos botones representan ¾ (tres cuartas) partes de un conjunto de 8 botones?
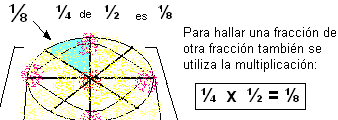
¿Quieres saber qué parte del pastel se comió tu hermanita si le sirvieron ¼ (un cuarto) de la mitad del pastel?
En los ejemplos anteriores has visto diferentes representaciones para la multiplicación de fracciones, en todos los casos el producto se calcula de la misma forma:
Observa que:
En todos los casos se han multiplicado las fracciones multiplicando numerador por numerador y denominador por denominador.
Veamos otros ejemplos:
Halla el producto de las siguientes fracciones:
¿Cómo los resolvemos?:
En resumen:
- La multiplicación de fracciones se realiza multiplicando los numeradores y multiplicando los denominadores entre sí. Es conveniente, antes de calcular el producto simplificar tanto como sea posible de lo contrario deberás hacerlo en la fracción resultante.
De forma general:
División de fracciones comunes
Recíproco de una fracción
Antes de comenzar el estudio de la división de fracciones, es necesario que aprendas qué es el recíproco de una fracción, lo necesitarás en el procedimiento a seguir para dividir.
Definición 1
El recíproco de una fracción es la fracción
donde
.
Dada una fracción, para formar su recíproco, basta invertir sus términos.
Ejemplos de recíproco
Halla el recíproco de:
a) 1/3 (uno sobre tres)
b) 2
c) 7/4 (siete sobre cuatro)
d) 0,5
Respuestas:
a) 1/3 (uno sobre tres) es igual a 3/1 (tres sobre uno). Invirtiendo el numerador y el denominador. El recíproco de 1/3 (uno sobre tres) es igual a 3.
b) 2 es igual a ½ . El recíproco de 2 es ½ (un medio).
c) 7/4 (siete sobre cuatro) es igual a 4/7 (cuatro sobre siete). El recíproco de 7/4 (siete sobre cuatro) es 4/7 (cuatro sobre siete).
d) 0,5 igual a 5/10 (cinco sobre diez). Se escribe la expresión decimal como fracción. El recíproco de 5/10 (cinco sobre diez) es 10/5 (diez sobre cinco) que es igual a 2.
En los números naturales la división significa repartir en partes iguales, con las fracciones también se le puede dar esa interpretación y resolver situaciones prácticas, por ejemplo:
Tienes 5 naranjas y las picas exactamente a la mitad ¿cuántas partes tienes ahora?
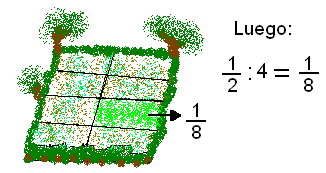
La mitad de un huerto escolar la divides en cuatro partes iguales para sembrar lechugas en una de ellas, ¿qué parte del terreno se dedicará a ese tipo de hortalizas?
Para hallar qué parte es un conjunto de otro, debes dividir. Luego también podemos darle este significado a la división de fracciones , por ejemplo:
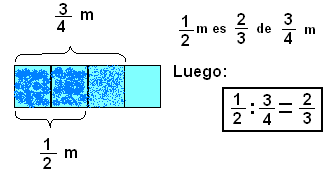
¿Qué parte es ½ m de tela de ¾ m?
Independientemente de las diferentes interpretaciones que puede tener la división, para calcular existe un único procedimiento como podemos observar a continuación:
En todos los casos se han dividido las fracciones reduciéndolas a una multiplicación donde el segundo factor es el recíproco del divisor.
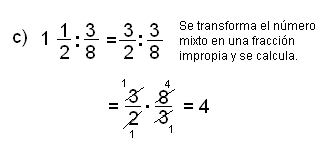
Ejemplos de división
Halla el cociente:
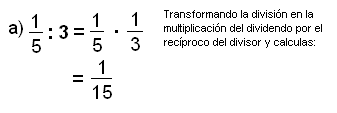
Para resolverlos:
En resumen:
- La división de fracciones se realiza transformándola en una multiplicación en la cual el primer factor es el dividendo y el segundo es el recíproco del divisor. Luego se procede como en la multiplicación.
De forma general:
Fuentes
- Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, 1990.
- Profesor en linea disponible en www.profesorenlinea.cl. Consultada el 18 de abril de 2011.