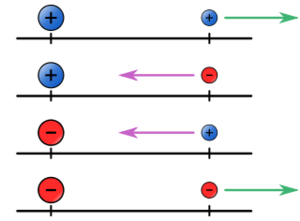
Multiplicación y división de números negativos
| ||||||
Multiplicación y división de números negativos. Multiplicación: se dice que es la abreviatura de la adición de sumandos iguales. Se les relaciona con las palabras: producto, doble, triple o producto cartesiano de conjuntos: 9 + 9 + 9 + 9 + 9 es lo mismo que 5 veces 9 ; es decir, 5 X 9, sus elementos son: factores y producto.
División: Algunos piensan que esta operación es egoísta, porque se relaciona con separar. Al contrario, es una expresión clara de justicia. Ella se encarga de repartir y lo hace siempre en partes iguales. Sus elementos son: dividendo, divisor y cociente.
Sumario
Reseña histórica
Los números enteros positivos y negativos, son el resultado natural de las operaciones suma y resta. Su empleo, aunque con diversas notaciones, se remonta a la antigüedad.
El nombre de enteros se justifica porque estos números ya sean positivos o negativos, siempre representaban una cantidad de unidades no divisibles (por ejemplo, personas).
No fue sino hasta el siglo XVII que tuvieron aceptación en trabajos científicos europeos, aunque matemáticos italianos del renacimiento como Tartaglia y Cardano los hubiesen ya advertido en sus trabajos acerca de solución de ecuaciones de tercer grado. Sin embargo, la regla de los signos ya era conocida previamente por los matemáticos de la India.
La multiplicación era considerada una operación muy difícil en Europa antes del siglo XVI, pues aún se utilizaban los números romanos y, en este sistema de numeración las operaciones con números grandes son más difíciles que con el sistema decimal posicional.
Multiplicación
Propiedades de la multiplicación
La multiplicación de números enteros tiene también propiedades similares a la de números naturales:
- Propiedad asociativa. Dados tres números enteros a, b y c, los productos (a × b) × c y a × (b × c) son iguales.
- Propiedad conmutativa. Dados dos números enteros a y b, los productos a × b y b × a son iguales.
- Propiedad distributiva. Establece que multiplicar una suma por un número da el mismo resultado que multiplicar cada sumando por el número y después sumar todos los productos.
- Elemento neutro. Todos los números enteros a quedan inalterados al multiplicarlos por 1: a × 1 = a.
Ejemplos
Propiedad asociativa:
[ (−7) × (+4) ] × (+5) = (−28) × (+5) = −140
(−7) × [ (+4) × (+5) ] = (−7) × (+20) = −140
Propiedad conmutativa:
(−6) × (+9) = −54
(+9) × (−6) = −54
La suma y multiplicación de números enteros están relacionadas, al igual que los números naturales, por la propiedad distributiva:
Propiedad distributiva:
Dados tres números enteros a, b y c, el producto a × (b + c) y la suma de productos (a × b) + (a × c) son idénticos.
Elemento neutro
a · 1 = a
La multiplicación de números enteros, al igual que la suma, requiere determinar por separado el signo y valor absoluto del resultado.
En la multiplicación de dos números enteros se determinan el valor absoluto y el signo del resultado de la siguiente manera:
El valor absoluto es el producto de los valores absolutos de los factores.
El signo es "+" si los signos de los factores son iguales, y "−" si son distintos.
Para recordar el signo del resultado, también se utiliza la regla de los signos:
Regla de los signos
(+) × (+) = (+) Más por más igual a más.
(+) × (−) = (−) Más por menos igual a menos.
(−) × (+) = (−) Menos por más igual a menos.
(−) × (−) = (+) Menos por menos igual a más.
Ejemplos
(+4) × (−6). El signo de los factores es distinto, así que el signo del resultado es "−". El producto de los valores absolutos es 4 × 6 = 24. O sea: (+4) × (−6) = −24.
(+5)×(+3). El signo de los factores es idéntico, así que el signo del resultado es "+". El producto de los valores absolutos es 5 × 3 = 15. O sea: (+5) × (+3) = +15.
(−7) × (+8). El signo de los factores es distinto, luego el signo del resultado es "−". El producto de los valores absolutos es 7 × 8 = 56. O sea: (−7) × (+8) = −56.
(−9)×(−2). El signo de los factores es el mismo, así que el signo del resultado es "+". El producto de los valores absolutos es 9 × 2 = 18. O sea:(−9) × (−2) = +18.
División
Las reglas que se obtuvieron para la multiplicación funcionan perfectamente en el caso de la división de los números racionales.
La división de signos iguales da un signo positivo y la división de signos diferentes da un signo negativo.
En la división de fracciones, al cambiar de lugar al divisor y al dividendo (numerador y denominador), se modifica el resultado de la división, pero no el signo.
Referencias
- Artículo: Propiedades de la multiplicación. Disponible en: "www.kalipedia.com". Consultada el 6 de junio de 2011.
- Artículo: Básica. Disponible en: "www.si-educa.net". Consultada el 6 de junio de 2011.
- Cursos: Contenidos-Libros. Disponible en: "www.conevyt.org.mx". Consultada el 7 de junio de 2011.
- Contenidos de matemática. Disponible en: "www.rena.edu.ve". Consultada el 7 de junio de 2011.
- Artículo: Notas hacerca de la historia de los números. Disponible en: "boards5.melodysoft.com". Consultada el 7 de junio de 2011.
- Artículo: Tema 8vo Breve historia de los numeros negativos. Disponible en: "www.rimed.cu". Consultada el 9 de junio de 2011.
- Artículo: Multiplicación de números negativos. Disponible en: "es.wikipedia.org". Consultada el 9 de junio de 2011.
- Artículo: Números enteros. Propiedades algebráicas. Disponible en: "es.wikipedia.org". Consultada el 9 de junio de 2011.
Fuente
Libro de texto de Matemática de 7mo grado. Editorial Pueblo y Educación, 1989.