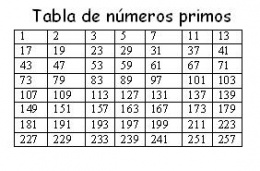
Número primo
| ||||||
En matemática, particularmente en aritmética o teoría de números, un número primo es un número entero que admite exactamente dos divisores: él mismo y 1. Su estudio está ligado a la divisibilidad tan útil en la forja de sistemas algebraicos finitos y la definición de representante canónico de un número racional. En la matemática de la educación básica, basta tomar un número primo como como número natural mayor que 1 que tiene sólo dos divisores distintos. [1] [2]
Ejemplo: El número 5, que sólo es divisible por 5 y por 1, es un número primo.
Entre tantos otros, son números primos: 3; 7; 11; 23; 29; etc
Sumario
Definiciones alternativas
- A un número entero p>1 se llama número primo, o simplemente, primo, en caso de que no exista divisor q de p que cumpla p>q> 1. Cuando un número entero, mayor que 1, no es primo, se expresa que es número compuesto.
- Se llama número primo a cualquier número entero h que es divisible exactamente por cuatro factores: 1,-1,h,-h, según la idea de Edmund Landau, que aparece en su célebre obra "Teoría elemental de números", publicada en 1927. [4]
- Sea R un anillo. Un elemento k de R, no nulo y no invertible, se llama primo, cuando cada vez que k divida el producto de dos elementos de R, también divide a uno de sus factores.[5]. Así, 2 es primo; puesto si 2|mn, por lo menos uno de ellos tiene que ser par, si ninguno fuera el producto de impares sería impar. 6 no es primo pues divide a 36 = 4x9, pero no divide a ninguno de tales factores.
Varía con los conjuntos numéricos
El concepto de número primo depende del concepto de divisibilidad y del conjunto donde se trabaja. Por ejemplo, el número 5, como gaussiano entero no es primo; pues se puede expresar como el producto (2+i)x(2-i) = (1+2i)x(1-2i) = 5x1 [6]. El 7 es un entero primo, también lo es como gaussiano entero primo; en cambio en el cuerpo cuadrático Q(21/2) no es primo, pues 7 = (3 + 21/2) (3 - 21/2) = 9 - 2.
Números primos entre sí
Números primos entre sí o números primos relativos, Son los que no tienen más factor común que la unidad.
Ejemplo: el 8 y el 9 son primos entre sí porque la unidad es el único número que los divide a los dos; sin embargo puedes notar que ni el 8 ni el 9 son primos absolutos. El 5, el 18 y el 21 son también primos entre sí, porque el 3 que divide al 18 y al 21, no divide al 5 y resulta que el único número que divide a los tres es el 1, el 18 y el 21 no son primos entre sí porque ambos son divisibles por 3.
Principios fundamentales
- La serie de los números primos es ilimitada.
Esto quiere decir que no se puede señalar un número primo como el mayor de todos, como el último, púes siempre habrá otro mayor que él.
- El menor divisor, aparte de 1, de un número natural es primo.
En efecto, si suponemos que dicho divisor no es primo, sería compuesto y entonces podría descomponerse en el producto de dos factores menores que él. Si el menor de estos dos fuera primo, se confirmaría lo dicho, si no lo fuera, se podría descomponer en otros dos factores y así sucedería siempre, como los factores serían cada vez más pequeños, forzosamente tendríamos que llegar a un factor que no se pudiera descomponer, es decir que fuera primo, comprobándose lo dicho al principio.
- Un número es primo si no es divisible por los números primos cuyos cuadrados sea menores que él.
En este caso, si fuera compuesto, su menor factor tendría que ser un número primo mayor que esto, ahora bien si ese número primo, multiplicado por él mismo (elevado al cuadrado) da un producto mayor que el número dado, no es posible que multiplicado por otro número mayor que él, pueda resultar el número dado.(Ley de monotonía de la multiplicación.).
Ejemplo:
Sea el número 109. Los números primos cuyos cuadrados son menores que él son 2; 3; 3; 5 y 7, pues el siguiente número primo es 11 y su cuadrado es 121, mayor que 109, como 109 no es divisible por 2; 3; 5 ni 7 podemos afirmar que es primo. Si no lo fuera, su menor factor que tiene que ser primo de acuerdo con el segundo principio, sería por lo menos 11, ahora bien, si 11 x 11 es mayor que 10, si multiplicamos 11 por otro número mayor el producto no puede ser igual a 10, por lo tanto 11 no es factor de 10, lo mismo sucederá con los números primos mayores que 11 en consecuencia, podemos afirmar que 109 es un número primo.
- Todo número compuesto puede expresarse como un producto indicado de factores primos y sólo uno.
Al dividir un número compuesto cualquiera por su menor factor (primo) puede resultar que el cociente (el otro factor) sea primo o no. Si es primo queda el número descompuesto en dos factores primos, si no lo es, se podrá descomponer en un factor primo y otro que será primo o no, si es primo quedará el número descompuesto en tres factores primos (Ley disociativa de la multiplicación). Si no lo es podrá descomponerse a su ve. Siguiendo este procedimiento llegaremos al final a tener una serie de factores primos cuyo producto total sea el número primitivo, así queda éste expresado como un producto de factores primos.
Proposiciones
- Dados b y m enteros mayores que 1. Si bm-1 es primo, entonces b=2 y m es primo. Ejemplos: 3, 31, 127
- Dados b y m enteros no menores que 2. si bm+1 es primo, entonces b es par y m es una potencia de 2 con exponente entero positivo. Tal como 17. [7]
- Cualquier primo impar es la diferencia de los cuadrados de dos números consecutivos. Ejemplos:11 = 36-25; 13 = 49-36; 23=144-121; 47=576-529, etc.
- Un número natural primo de la forma 4k+1, aquí k es natural, se expresa como la suma de los cuadrados de dos números naturales; ejemplos: 4×3+1 = 13 = 9 +4; 4×10+1=41 = 25+16; pero 21 por no ser primo no es suma de cuadrados, tampoco 19 que es primo no es suma de cuadrados, por no tener la forma 4h+1, para h natural.
Modo de reconocer un número primo
Para reconocer si un número dado es o no primo se investiga si es divisible por los números primos desde el 2 en adelante (2; 3; 5; 7, etc.). Si se llega, sin obtener cociente exacto, a una división cuyo cociente sea menor o igual que el divisor, el número dado es primo. Si alguna división es exacta el número no es primo.
Descomposición de un número en sus factores primos
Descomponer un número dado en sus factores primos es hallar el producto indicado de factores primos equivalente a dicho número. Regla: Se divide el número dado por su menor factor primo; el cociente se divide por su menor factor primo; el nuevo cociente se divide por su menor factor primo y así sucesivamente hasta llegar a un cociente primo que dividido por sí da la unidad como cociente. El producto indicado de todos los divisores utilizados es la descomposición en factores del número dado.
Ejemplo: Descomponer el número 90 en sus factores primos.
Prácticamente disponemos de la operación así: 
Explicación:
Escribimos el número 90, pasamos una raya vertical a su derecha, vemos si es divisible por 2, como lo es ponemos el 2 del otro lado de la raya y al mismo nivel del 90. Hallamos la mitad de 90, lo cual da 45. Vemos si este es divisible por 3, ponemos el 3 debajo del 2 anterior y dividimos 45 por 3, el resultado es 15, este 15 lo ponemos debajo del 45, vemos si tiene tercera, como la tiene, escribimos otro 3 debajo del anterior, hallamos la tercera y obtenemos 5, no tiene tercera, vemos si tiene quinta, como tiene quinta escribimos el 5 debajo del último 3, se divide el número `por 5 y queda 1. Ahí termina la operación.
Resulta por tanto:
90 = 2 x 3 x 3 x 5
Y como: 3 x 3 = 32
Lo que se escribe es: 90 = 2 x 32 x 5
Referencias y notas
- ↑ Flavio Vega Villanueva Dr. en CC: MM.: Matemática 1. Editorial Colegio Militar Leoncio Prado, primera edición, La Perla Callao
- ↑ La definición concilia con la dada por Vinogradov en su obra "fundamentos de la teoría de números"
- ↑ Niven y Zuckerman: Introducción a la teoría de números ISBN 968-18-069-7, pág.
- ↑ Enzo Gentile: Aritmética elemental, edición de la OEA, Washingron D.C. (1985)
- ↑ Abramo Hefez: Curso de álgebra vol1. Imca, Lima (2001)
- ↑ Comprobar estos resultados, donde i es la unidad imaginaria
- ↑ Abramo Hefez: Álgebra I vol. 1 IMCA Lima (2001)
Véase también
Fuentes
- Sócrates Rosell, F.: Volumen I. La Habana: Editorial Pedagógica, segunda edición.