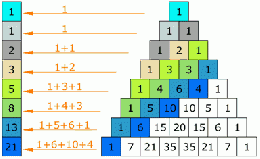
Números de Fibonacci
| ||||
Números de Fibonacci. Son los números que conforman la sucesión de Fibonacci. Una sucesión de números muy conocida y usada en matemáticas .Siendo el constructor inicial de una forma clásica, Leonardo de Pisa, más conocido como Fibonacci.
Sumario
Definición
Se llaman números de Fibonacci a aquellos que son términos de la sucesión de números naturales donde cada número se calcula sumando los dos anteriores a él.
La sucesión de Fibonacci es la siguiente sucesión de números enteros positivos:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...[1]
Historia
La sucesión de Fibonacci es una secuencia de números enteros inventada por matemáticos hindúes hacia el año 1135 y descrita por primera vez en Europa gracias a Leonardo Fibonacci.
Esta sucesión fue descrita por Fibonacci como la solución a un problema de la cría de conejos.
Muchas propiedades de la sucesión de Fibonacci fueron descubiertas por Édouard Lucas, responsable de haberla denominado como se la conoce en la actualidad.
Esta serie ha tenido popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores como Béla Bartók u Olivier Messiaen la han utilizado para la creación de acordes y de nuevas estructuras de frases musicales.
La sucesión de Fibonacci ha tenido intrigados a los matemáticos durante siglos, debido a su tendencia a presentarse en los lugares más inopinados, pero sobre todo, porque el más novel de los aficionados en teoría de números, aun con conocimientos poco más allá de aritmética elemental, puede aspirar a investigarla y descubrir curiosos teoremas inéditos, de los que parece haber variedad inagotable.
Ecuación recurrente
La sucesión de Fibonacci se puede determinar como mediante ecuación recurrente [2] es xn = xn-1 + xn-n donde: xn es el término - n-ésimo, xn-1 es el término anterior o de orden (n-1); xn-2 es el anterior al de orden n-1. Y los valores iniciales 1, 1. Por ejemplo el sexto término se calcula así:
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8.
Propiedades básicas
La sucesión de Fibonacci tiene muchas propiedades curiosas:
- La suma de los n primeros términos es: a1 + a2 +... + an = an+2 - 1, para n≥2
- La suma de los términos impares es: a1 + a3 +... + a2n-1 = a2n
- La suma de los términos pares es: a2 + a4 +... + a2n = a2n+1 - 1
- La suma de los cuadrados de los n primeros términos es: a12 + aa2 +... + a n2 = anan+1
- Propiedad hereditaria: Si n es divisible por m entonces an es divisible por am. El cuarto es 3, el octavo es 21; 4 divide 8, luego 3 divide 21.
- Dos números consecutivos de Fibonacci son primos entre sí.
- La propiedad interesante de esta sucesión es que el cociente de dos números consecutivos de la serie se aproxima a la razón áurea cuando n se hace cada vez más grande. Esto es: an+1/an tiende a (1 + ð 5)/2
Aplicaciones
Aparte de que esta sucesión tiene varias propiedades interesantes, lo más curioso de esta es su presencia en la naturaleza. La sucesión de Fibonacci está muy ligado a la vida y estos hechos lo demuestran:
- Los machos de una colmena de abejas tienen un árbol genealógico que cumple con esta sucesión. El hecho es que los zánganos, el macho de la abeja, no tiene padre (1), pero sí que tiene una madre (1, 1), dos abuelos, que son los padres de la reina (1, 1, 2), tres bisabuelos, ya que el padre de la reina no tiene padre (1, 1, 2, 3), cinco tatarabuelos (1, 1, 2, 3, 5), ocho tatarabuelos (1, 1, 2, 3, 5, 8) y así sucesivamente, cumpliendo con la sucesión de Fibonacci.
- En la mano humana también se encuentra esta recurrencia, la longitud del metacarpo es la suma de las dos falanges proximales y la longitud de la primera falange es la suma de las dos falanges distales.
- El número de pétalos de una flor es generalmente un término de Fibonacci. Hay flores con 2 pétalos, 3, 5, 8, 13, 21, 34, pero muy rara vez es un número que no esté en esta sucesión.
- Las espirales de los girasoles.
- Las espirales de las piñas.
- La altura de la cadera y la altura de la rodilla.
- La altura de un ser humano y la altura de su ombligo.
- La mona lisa
Y muchas otras cosas…
El problema de los conejos
La sucesión fue descrita por Fibonacci como la solución a un problema de la cría de conejos:
El ejercicio de Fibonacci pregunta cuántas parejas de conejos habrá en una granja luego de 12 meses, si se coloca inicialmente una sola pareja y se parte de las siguientes premisas:
- Los conejos alcanzan la madurez sexual a la edad de un mes.
- En cuanto alcanzan la madurez sexual los conejos se aparean y siempre resulta preñada la hembra.
- El periodo de gestación de los conejos es de un mes.
- Los conejos no mueren.
- La hembra siempre da a luz una pareja de conejos de sexos opuestos.
- Los conejos tienen una moral y un instinto de variedad genética muy relajados y se aparean entre parientes.
El proceso de crecimiento de la población de conejos es mejor descrito con la siguiente ilustración:
Como se puede observar el número de parejas de conejos por mes está determinado por la sucesión de Fibonacci.
Nim de Fibonacci
El juego conocido como el Nim de Fibonacci, consiste en ir retirando cuentas de una pila que inicialmente contiene n fichas. Los jugadores actúan por turno. En la primera jugada no es lícito retirar la pila completa, aunque sí en las sucesivas, siempre que se respeten las siguientes reglas:
- En cada turno es obligatorio retirar al menos una ficha.
- Ningún jugador puede retirar más del doble del número de fichas que haya retirado su oponente en el turno anterior.
- Gana la partida quien retire la última ficha.
Si n es un número de Fibonacci, el segundo jugador puede ganar siempre; en cambio si no es así el ganador, si sigue la estrategia correcta, será el primero. Si una partida comienza con 20 fichas (que no es un número de Fibonacci), ¿cuántas debe retirar el primer jugador para asegurarse la victoria?
Descomponemos el número 20 en números de Fibonacci, comenzando por el mayor posible (el 13) sumando después el mayor posible (5) y después el siguiente (2). Así que 20=13+5+2 es la descomposición buscada. Todo número entero puede descomponerse de forma única como una suma de números de Fibonacci; tal descomposición no contendrá nunca números F consecutivos.
El último número, el 2, es el número de cuentas que ha de retirar el primer jugador para ganar. El segundo queda imposibilitado por las reglas a tomar más del doble de 2, por consiguiente no puede reducir la pila (que ahora tiene 18 cuentas) al número F más cercano (el 13). Supongamos que retire 4; la pila tendrá ahora 14 cuentas, número que se expresa como 14=13+1 en números F, por lo que el primero retirará ahora 1 cuenta. Prosiguiendo con esta estrategia, ganará.