Paralelismo y Perpendicularidad
| ||||
Paralelismo y perpendicularidad.
Definición
Sean las rectas r1 y r2 de pendientes m1 y m2 respectivamente, se cumple que:
a) r1 // r2 si y solo si m1 = m2
b) r1 ↓ r2 si y solo si m2 = - 1/m1
Demostración
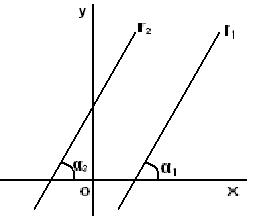
Si r1 // r2
se cumple que:
ɑ1 = ɑ2 por ser correspondientes
luego
tan ɑ1 = tan ɑ2
por tanto
m1 = m2 (Condición de paralelismo)
como los pasos son reversibles se demuestra que si m1 = m2,
entonces r1 // r2 y queda demostrado el inciso a).
b) r1 ↓ r2
se cumple que:
ɑ2 = 90o + ɑ1 ángulo exterior a un triángulo
luego
tan ɑ2 = tan ( 90o + ɑ1 )
tan ɑ2 = - cot ɑ1 = -1/tan ɑ1
por tanto m2 = - 1/m1 (condición de perpendicularidad)
como los pasos son reversibles se demuestra que si m2 = - 1/m1, entonces r1 ↓ r2 y queda demostrado el inciso b.
Ejercicio Resuelto
Muestra que el triángulo cuyos vértices son A(2; -3), B(5; -2) y C(4;1) es rectángulo.
m= y2 - y1 / x2 - x1
mAB = -2 - (-3)/ 5-2
mAB = -2 + 3 / 3
mAB = 1/3
m= y2 - y1 / x2 - x1
mBC = 1 - (-2) / 4 - 5
mBC = 1 + 2 / - 1
mBC = 3 / -1
Por lo que
MAB = - 1/MBC
El triángulo es rectángulo en el vértice B.
Veáse también
Fuente
- Colectivo de autores. Matemática 11no grado. Editorial Pueblo y Educación. 1990.
- Libro de texto Matemática 10mo grado. Editorial Pueblo y Educación. 1990.
- Cuaderno Complementario. Matemática 9 no grado. Editorial Pueblo y Educación. 2005.