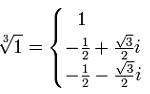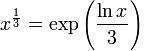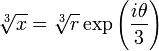Raíz cúbica
| ||||||
Raíz cúbica. Es la cantidad que se ha de multiplicar por sí misma 3 veces para obtener como resultado el radicando o número que acompaña al símbolo matemático de raíz.
Cubo de un número
En aritmética y álgebra, el cubo de un número x es igual a la tercera potencia, lo cual es correspondiente al resultado de multiplicar un número por sí mismo tres veces.
Números reales
Habitualmente un número real posee tres raíces cúbicas, una raíz es correspondiente a un real mientras que las otras dos a números complejos. Un número complejo representa la adición de un número real a un número imaginario.
Si x e y son números reales, entonces habrá una sola solución tal que la ecuación posea además una única solución, esta corresponderá a un real. Si se utiliza esta definición, la raíz cúbica de un número negativo es además un número negativo. Siendo así, el principio de la raíz cúbica de x se constituye por: Si x e y son complejos, se puede decir que hay tres soluciones (siempre y cuando x sea no nulo) y así x posee tres raíces cúbicas, una es raíz real y las otras son complejas, en la forma de par conjugado.
Estas dos raíces tienen relación con todas las otras raíces cúbicas de otros diferentes números. Entonces si un número es correspondiente a la raíz cúbica de un número real las raíces cúbicas podrán ser calculadas mediante la multiplicación del número por las raíces de la raíz cúbica de uno
Si se hace referencia a los números complejos, el valor principal de las raíces cúbicas se define de esta forma:
Donde ln(x) es el logaritmo natural. Si se escribe x como:
r es correspondiente a un número real positivo y θ cae en el rango:
Por lo cual la raíz cúbica es la siguiente:
Esto quiere decir que si se procede a tomar la raíz cúbica de un complejo se está tomando la raíz cúbica del radio y el ángulo polar se está dividiendo entonces en tres partes, de modo que se definen las tres raíces. Con dicha definición, la raíz cúbica de un número negativo será un número complejo.
Calcular la raíz cúbica de un número
1. La raíz cúbica se calcula de forma semejante a la raíz cuadrada, pero se separan los dígitos del radicando en agrupaciones de tres cifras. Por ejemplo: 16387064 se separaría en: 16’387’064. 2. Después se procede a calcular un número entero que cuando se eleve al cubo se aproxime lo más posible al número del primer grupo (comenzando siempre por la izquierda).
En el ejemplo el primer número es 16 y el número entero que elevado al cubo se aproxima más a 16 es el número 2. Entonces 2 es la primera cifra de la raíz.
3. Luego se eleva al cubo esta cifra y se resta inmediatamente el número del primer grupo.
En el ejemplo 23 = 8 y restándolo del número del primer grupo que es 16 obtenemos que 16 – 8 = 8.
4. Se procede a colocar al lado del resto obtenido anteriormente el número del próximo grupo.
En el ejemplo queda la siguiente cifra: 8387.
5. Posteriormente es necesario realizar el cálculo de un número a, ejecutando las operaciones:
Aproximándose lo más posible al número obtenido en el punto 4. El número a, será el siguiente dígito de la raíz. En el ejemplo esto es correspondiente al número 5.
6. Se resta ahora este número al número que obtuvimos en el punto 4. Por lo cual: 8387- 7625 = 762. 7. Se realiza nuevamente el punto 4. En el ejemplo: 762064 8. Se repite el quinto paso y el número que se obtenga será el subsiguiente número de la raíz.
En el ejemplo sería el 4, porque
9. Se procede a realizar nuevamente el sexto punto. En el ejemplo 762064-762064 = 0
La raíz es exacta ya que el resto es cero.