Diferencia entre revisiones de «Matrices lógicas programables»
(Página creada con '{{Objeto|nombre=Matrices Lógicas Programables|imagen=Matriz_p.JPG|descripcion= Matriz programable}} <div align="justify"> ''' Matrices Lógicas Programables''':Una matriz e...') (Etiqueta: no tiene enlaces internos) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 10 ediciones intermedias de 5 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | {{Objeto|nombre=Matrices Lógicas Programables|imagen= | + | {{Objeto|nombre=Matrices Lógicas Programables|imagen=MatricesL.jpeg|descripcion= Matriz programable}} |
| − | + | ||
| − | ''' Matrices Lógicas Programables''' | + | ''' Matrices Lógicas Programables'''. Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general, suelen ser números ordenados en filas y columnas. |
| − | Se llama matriz de orden m × n; a un conjunto rectangular de elementos a ij dispuestos en m filas y en n columnas. El orden de una matriz también se denomina dimensión o tamaño , siendo m y n números naturales. | + | Se llama [[matriz]] de orden m × n; a un conjunto rectangular de elementos a ij dispuestos en m filas y en n columnas. El orden de una matriz también se denomina dimensión o tamaño , siendo m y n números naturales. |
| − | Los dispositivos lógicos programables incorporan una matriz lógica genérica, que puede programarse de forma que el dispositivo (circuito integrado)realice las funciones que se desee. | + | |
| + | Los dispositivos [[lógicos]] programables incorporan una matriz lógica genérica, que puede programarse de forma que el dispositivo (circuito integrado)realice las funciones que se desee. | ||
== Estructura de una matriz == | == Estructura de una matriz == | ||
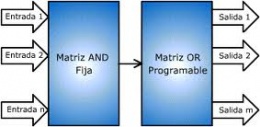
Normalmente la estructura programable principal consiste en una estructura combinacional, formada por una matriz de puertas AND, a cuyas entradas se conectan las entradas del dispositivo tanto de forma directa como negada. Según el tipo de dispositivo del que dispongamos,esta primera matriz estará o no seguida de una segunda matriz formada en el caso más general por puertas OR, de manera que pueda realizarse fácilmente una suma de productos. | Normalmente la estructura programable principal consiste en una estructura combinacional, formada por una matriz de puertas AND, a cuyas entradas se conectan las entradas del dispositivo tanto de forma directa como negada. Según el tipo de dispositivo del que dispongamos,esta primera matriz estará o no seguida de una segunda matriz formada en el caso más general por puertas OR, de manera que pueda realizarse fácilmente una suma de productos. | ||
Las matrices programables están formadas por fusibles, que el usuario puede eliminar o dejar intactos para generar la lógica deseada. Para simplificar la representación de estas estructuras, las diferentes entradas de una puerta AND se representan con una sola línea denominada línea producto. En la figura 1a se representan cómo se sitúan los fusibles y en la figura 1b la representación gráfica,donde se observa que un fusible intacto se representa con una 'X' y un fusible eliminado sin ningún símbolo especial en la unión correspondiente. | Las matrices programables están formadas por fusibles, que el usuario puede eliminar o dejar intactos para generar la lógica deseada. Para simplificar la representación de estas estructuras, las diferentes entradas de una puerta AND se representan con una sola línea denominada línea producto. En la figura 1a se representan cómo se sitúan los fusibles y en la figura 1b la representación gráfica,donde se observa que un fusible intacto se representa con una 'X' y un fusible eliminado sin ningún símbolo especial en la unión correspondiente. | ||
| − | [[Image: Fgr1.JPG |thumb| | + | [[Image: Fgr1.JPG |thumb|left|367x309px|Matrices programables]] |
| + | |||
| + | == Propiedades == | ||
| + | |||
| + | Sólo existe matriz inversa de una matriz cuadrada si ésta es regular. | ||
| + | La matriz inversa de una matriz cuadrada, si existe, es única. | ||
| + | Entre matrices NO existe la operación de división, la matriz inversa realiza funciones análogas. | ||
| + | == Operaciones con matrices == | ||
| + | ===Suma de matrices=== | ||
| + | La suma de dos matrices A = (a ij )m×n y B = (b ij )p×q de la misma dimensión (equidimensionales) : m = p y n = q es otra matriz C = A+B = (c ij )m×n = (a ij +b ij ) | ||
| + | Es una ley de composición interna con las siguientes propiedades: | ||
| + | ==== Asociativa ==== | ||
| + | A+(B+C) = (A+B)+C | ||
| + | |||
| + | ==== Conmutativa ==== | ||
| + | A+B = B+A | ||
| + | ==== Elemento neutro ==== | ||
| + | |||
| + | ( matriz cero 0 m×n ) , 0+A = A+0 = A | ||
| + | ==== Elemento simétrico ==== | ||
| + | ( matriz opuesta -A ) , A + (-A) = (-A) + A = 0 | ||
| + | Al conjunto de las matrices de dimensión m×n cuyos elementos son números reales lo vamos a representar por M m×n y como hemos visto, por cumplir las propiedades anteriores, ( M, + ) es un grupo abeliano. | ||
| + | ===Producto de un número real por una matriz=== | ||
| + | Para multiplicar un escalar por una matriz se multiplica el escalar por todos los elementos de la matriz, obteniéndose otra matriz del mismo orden. | ||
| + | Es una ley de composición externa con las siguientes propiedades : | ||
| + | ==== Producto de matrices ==== | ||
| + | Dadas dos matrices A = (a ij )m×n y B = (b ij )p×q donde n = p, es decir, el número de columnas de la primera matriz A es igual al número de filas de la matriz B , se define el producto A·B de la siguiente forma : | ||
| + | El elemento a que ocupa el lugar (i, j) en la matriz producto se obtiene sumando los productos de cada elemento de la fila i de la matriz A por el correspondiente de la columna j de la matriz B. | ||
| + | MATRIZ INVERSA | ||
| + | Se llama matriz inversa de una matriz cuadrada An y la representamos por A -1 , a la matriz que verifica la siguiente propiedad : A -1 ·A = A·A -1 = I | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Aplicaciones == | == Aplicaciones == | ||
| + | Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Además de su utilidad para el estudio de sistemas de ecuaciones lineales, las matrices aparecen de forma natural en geometría, estadística, economía, [[informática]], [[física]], etc. | ||
| + | La utilización de matrices constituye actualmente una parte esencial donde los lenguajes de programación, ya que la mayoría de los datos se introducen en los ordenadores como tablas organizadas en filas y columnas : hojas de cálculo, bases de datos. | ||
| − | + | == Fuentes == | |
| − | + | *Microelectronics, Jacob Millman, [[1979]] | |
| − | + | *Electrónica Digital. Julio Díaz Calvo. [[Editorial Pueblo y Educación]], [[1989]] | |
| − | + | *Circuitos Electrónicos Digitales II, Elías Muñoz Merino,Editorial Pueblo y Educación, [[1980]]. | |
| − | == | + | [[Category:Electrónica]][[Category:Electrónica digital]][[Category:Matrices]] |
| − | *Microelectronics, Jacob Millman, 1979 | ||
| − | *Electrónica Digital. Julio Díaz Calvo. Editorial Pueblo y Educación, 1989 | ||
| − | |||
| − | [[Category:Electrónica]] | ||
última versión al 19:36 22 jul 2019
| ||||
Matrices Lógicas Programables. Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general, suelen ser números ordenados en filas y columnas. Se llama matriz de orden m × n; a un conjunto rectangular de elementos a ij dispuestos en m filas y en n columnas. El orden de una matriz también se denomina dimensión o tamaño , siendo m y n números naturales.
Los dispositivos lógicos programables incorporan una matriz lógica genérica, que puede programarse de forma que el dispositivo (circuito integrado)realice las funciones que se desee.
Sumario
Estructura de una matriz
Normalmente la estructura programable principal consiste en una estructura combinacional, formada por una matriz de puertas AND, a cuyas entradas se conectan las entradas del dispositivo tanto de forma directa como negada. Según el tipo de dispositivo del que dispongamos,esta primera matriz estará o no seguida de una segunda matriz formada en el caso más general por puertas OR, de manera que pueda realizarse fácilmente una suma de productos. Las matrices programables están formadas por fusibles, que el usuario puede eliminar o dejar intactos para generar la lógica deseada. Para simplificar la representación de estas estructuras, las diferentes entradas de una puerta AND se representan con una sola línea denominada línea producto. En la figura 1a se representan cómo se sitúan los fusibles y en la figura 1b la representación gráfica,donde se observa que un fusible intacto se representa con una 'X' y un fusible eliminado sin ningún símbolo especial en la unión correspondiente.
Propiedades
Sólo existe matriz inversa de una matriz cuadrada si ésta es regular.
La matriz inversa de una matriz cuadrada, si existe, es única.
Entre matrices NO existe la operación de división, la matriz inversa realiza funciones análogas.
Operaciones con matrices
Suma de matrices
La suma de dos matrices A = (a ij )m×n y B = (b ij )p×q de la misma dimensión (equidimensionales) : m = p y n = q es otra matriz C = A+B = (c ij )m×n = (a ij +b ij ) Es una ley de composición interna con las siguientes propiedades:
Asociativa
A+(B+C) = (A+B)+C
Conmutativa
A+B = B+A
Elemento neutro
( matriz cero 0 m×n ) , 0+A = A+0 = A
Elemento simétrico
( matriz opuesta -A ) , A + (-A) = (-A) + A = 0
Al conjunto de las matrices de dimensión m×n cuyos elementos son números reales lo vamos a representar por M m×n y como hemos visto, por cumplir las propiedades anteriores, ( M, + ) es un grupo abeliano.
Producto de un número real por una matriz
Para multiplicar un escalar por una matriz se multiplica el escalar por todos los elementos de la matriz, obteniéndose otra matriz del mismo orden. Es una ley de composición externa con las siguientes propiedades :
Producto de matrices
Dadas dos matrices A = (a ij )m×n y B = (b ij )p×q donde n = p, es decir, el número de columnas de la primera matriz A es igual al número de filas de la matriz B , se define el producto A·B de la siguiente forma : El elemento a que ocupa el lugar (i, j) en la matriz producto se obtiene sumando los productos de cada elemento de la fila i de la matriz A por el correspondiente de la columna j de la matriz B.
MATRIZ INVERSA Se llama matriz inversa de una matriz cuadrada An y la representamos por A -1 , a la matriz que verifica la siguiente propiedad : A -1 ·A = A·A -1 = I
Aplicaciones
Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Además de su utilidad para el estudio de sistemas de ecuaciones lineales, las matrices aparecen de forma natural en geometría, estadística, economía, informática, física, etc. La utilización de matrices constituye actualmente una parte esencial donde los lenguajes de programación, ya que la mayoría de los datos se introducen en los ordenadores como tablas organizadas en filas y columnas : hojas de cálculo, bases de datos.
Fuentes
- Microelectronics, Jacob Millman, 1979
- Electrónica Digital. Julio Díaz Calvo. Editorial Pueblo y Educación, 1989
- Circuitos Electrónicos Digitales II, Elías Muñoz Merino,Editorial Pueblo y Educación, 1980.