Diferencia entre revisiones de «Ciclo euleriano»
(Página creada con «{{Definición |nombre=Ciclo euleriano |imagen=CicloEuleriano.png |tamaño= |concepto=Sea G un grafo sin vértices aislados. Un circuito que contiene todas las ari…») |
|||
| (No se muestran 6 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
{{Definición | {{Definición | ||
|nombre=Ciclo euleriano | |nombre=Ciclo euleriano | ||
| − | |imagen= | + | |imagen=CicloEuleriano1.png |
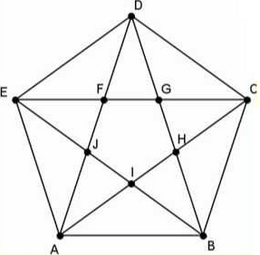
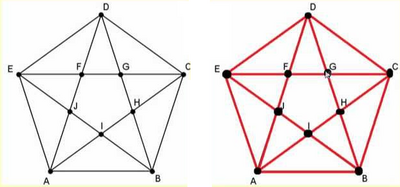
| + | |descripción=Recorrido {A,I}{I,H}{H,C}{C,G}{G,F}{F,E}{E,J}{J,I}{I,B}{B,H}{H,G}{G,D}{D,F}{F,J}{J,A}{A,B}{B,C}{C,D}{D,E}{E,A} | ||
|tamaño= | |tamaño= | ||
|concepto=Sea G un [[grafo]] sin [[vértice]]s aislados. Un circuito que contiene todas las [[arista]]s de G recibe el nombre de circuito euleriano. | |concepto=Sea G un [[grafo]] sin [[vértice]]s aislados. Un circuito que contiene todas las [[arista]]s de G recibe el nombre de circuito euleriano. | ||
| − | |||
}} | }} | ||
'''Ciclo euleriano'''. Un ciclo o circuito euleriano en la [[Teoría de Grafos]] es aquel camino que recorre todas las aristas de un grafo pasando una y sólo una vez por cada arco (arista) del grafo, siendo condición necesaria que regrese al vértice inicial de salida (ciclo = camino en un grafo donde coinciden vértice inicial o de salida y vértice final o meta). Es aquel ciclo que contiene todas las aristas de un grafo solamente una vez. | '''Ciclo euleriano'''. Un ciclo o circuito euleriano en la [[Teoría de Grafos]] es aquel camino que recorre todas las aristas de un grafo pasando una y sólo una vez por cada arco (arista) del grafo, siendo condición necesaria que regrese al vértice inicial de salida (ciclo = camino en un grafo donde coinciden vértice inicial o de salida y vértice final o meta). Es aquel ciclo que contiene todas las aristas de un grafo solamente una vez. | ||
| − | == | + | == Definición == |
| − | + | ||
| + | Sea G un grafo sin vértices aislados. Un circuito que contiene todas las aristas de G recibe el nombre de circuito euleriano. Es una trayectoria que empieza y termina en el mismo vértice y recorre cada arista exactamente una vez. | ||
| + | [[Archivo:CicloEuleriano.png |center|400px|]]<center><small>'''Recorrido {A,I}{I,H}{H,C}{C,G}{G,F}{F,E}{E,J}{J,I}{I,B}{B,H}{H,G}{G,D}{D,F}{F,J}{J,A}{A,B}{B,C}{C,D}{D,E}{E,A}'''.</small></center> | ||
== Historia == | == Historia == | ||
| − | |||
| − | == Véase | + | [[Leonhard Euler]] en [[1736]] plantea y resuelve la teoría de los ciclos eulerianos en el [[Problema de los puentes de Königsberg|problema de los siete puentes de la ciudad de Königsberg]] ([[Prusia]] oriental en el [[siglo XVIII]] y actualmente, [[Kaliningrado]], provincia rusa) dando origen a la [[Teoría de grafos|Teoría de los grafos]]. |
| + | |||
| + | == Véase también == | ||
*[[Grafo]] | *[[Grafo]] | ||
| Línea 22: | Línea 25: | ||
== Fuentes == | == Fuentes == | ||
| − | * Recorridos eulerianos. Gregorio Hernández Peñalver.[http://www.dma.fi.upm.es/personal/gregorio/matematica_discreta_II/71Euler.pdf] | + | * Recorridos eulerianos. Gregorio Hernández Peñalver. Disponible en:[http://www.dma.fi.upm.es/personal/gregorio/matematica_discreta_II/71Euler.pdf Departamento de Matemática Aplicada a las Tecnologías de la Información y las Comunicaciones (DMATIC), sección departamental de la Escuela Técnica Superior de Ingenieros Informáticos (ETSIINF), Universidad Politécnica de Madrid (UPM)]. Consultado el 29 de noviembre de 2021. |
| − | * Introducción a la teoría de grafos, Jesús García Miranda. [https://www.ugr.es/~jesusgm/Curso%202005-2006/Matematica%20Discreta/Grafos.pdf]. | + | * Introducción a la teoría de grafos, Jesús García Miranda. Disponible en:[https://www.ugr.es/~jesusgm/Curso%202005-2006/Matematica%20Discreta/Grafos.pdf Universidad de Granada]. Consultado el 29 de noviembre de 2021. |
| − | * Teoría de grafos. Una introducción histórica-técnica, Víctor Manuel Castaño Meneses.[https://www.ai.org.mx/sites/default/files/teoria_de_grafos_.pdf] | + | * Teoría de grafos. Una introducción histórica-técnica, Víctor Manuel Castaño Meneses. Disponible en:[https://www.ai.org.mx/sites/default/files/teoria_de_grafos_.pdf Academia de Ingeniería de México]. Consultado el 29 de noviembre de 2021. |
| − | [[Category:Matemáticas]][[Category:Informática]][[Category:Programación]] | + | [[Category:Matemáticas]] |
| + | [[Category:Informática]] | ||
| + | [[Category:Programación]] | ||
última versión al 12:24 2 dic 2021
| ||||||
Ciclo euleriano. Un ciclo o circuito euleriano en la Teoría de Grafos es aquel camino que recorre todas las aristas de un grafo pasando una y sólo una vez por cada arco (arista) del grafo, siendo condición necesaria que regrese al vértice inicial de salida (ciclo = camino en un grafo donde coinciden vértice inicial o de salida y vértice final o meta). Es aquel ciclo que contiene todas las aristas de un grafo solamente una vez.
Definición
Sea G un grafo sin vértices aislados. Un circuito que contiene todas las aristas de G recibe el nombre de circuito euleriano. Es una trayectoria que empieza y termina en el mismo vértice y recorre cada arista exactamente una vez.
Historia
Leonhard Euler en 1736 plantea y resuelve la teoría de los ciclos eulerianos en el problema de los siete puentes de la ciudad de Königsberg (Prusia oriental en el siglo XVIII y actualmente, Kaliningrado, provincia rusa) dando origen a la Teoría de los grafos.
Véase también
Fuentes
- Recorridos eulerianos. Gregorio Hernández Peñalver. Disponible en:Departamento de Matemática Aplicada a las Tecnologías de la Información y las Comunicaciones (DMATIC), sección departamental de la Escuela Técnica Superior de Ingenieros Informáticos (ETSIINF), Universidad Politécnica de Madrid (UPM). Consultado el 29 de noviembre de 2021.
- Introducción a la teoría de grafos, Jesús García Miranda. Disponible en:Universidad de Granada. Consultado el 29 de noviembre de 2021.
- Teoría de grafos. Una introducción histórica-técnica, Víctor Manuel Castaño Meneses. Disponible en:Academia de Ingeniería de México. Consultado el 29 de noviembre de 2021.