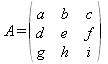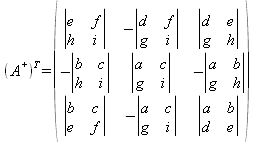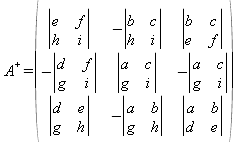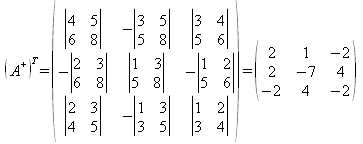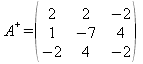Diferencia entre revisiones de «Matriz adjunta»
(→Obtención de adjuntas de matrices de orden 2 y 3) |
(→Ejemplos) |
||
| Línea 54: | Línea 54: | ||
En el caso de la matriz de orden 3: | En el caso de la matriz de orden 3: | ||
| − | + | {| class="wikitable" | |
| + | |- | ||
| + | |1||2||3 | ||
| + | |- | ||
| + | |3||4||5 | ||
| + | |- | ||
| + | |5||6||8 | ||
| + | |} | ||
| + | para calcular su ''A<sup>+</sup>'' se procede de manera análoga: | ||
| + | |||
| + | [[Archivo:EjemploTranspuestaMatrizAdjunta.gif|middle]] | ||
| + | |||
| + | [[Archivo:EjemploMatrizAdjunta.gif|middle]] | ||
==Importancia== | ==Importancia== | ||
Revisión del 11:38 13 dic 2016
| ||||||
Matriz adjunta. Es la matriz cuadrada de orden N que resulta de transponer los complementos algebraicos de otra matriz cuadrada del mismo orden.
Como el producto de la matriz original y su adjunta generan una matriz diagonal, cuyos elementos son el determinante de la matriz original, se usa para la obtención de la matriz inversa.
Sumario
Definición
Sea A una matriz cuadrada de orden N, se llama matriz adjunta de A y se simboliza A+ a la matriz:
donde a+i,j=(-1)j+iMj,i son los complementos algebraicos transpuestos correspondientes a cada elemento aj,i de A tal que el menor Mi,j se define por el determinante:
Obtención de adjuntas de matrices de orden 2 y 3
En el caso de las matrices cuadradas de orden 2 y 3 el mecanismo es más simple que en las de orden superior desde 4, aunque se sigue la misma idea de la definición.
Para el caso de A si tiene orden 2:
Su adjunta sería:
Para una matriz A de orden 3 es un poco más elaborado:
Se plantean los complementos algebraicos de cada elemento de A como sigue:
Esto sería la transpuesta de la matriz adjunta. Luego se intercambian filas por columnas para obtener A+:
Propiedades
Sea una matriz cuadrada A de orden N y su adjunta A+ se cumple entonces:
- (kA)+=kNA+
- (AB)+=A+B+
- AA+=A+A=|A|I
Ejemplos
Sea la matriz:
Mediante la forma de obtención expresada anteriormente A+ queda:
En el caso de la matriz de orden 3:
| 1 | 2 | 3 |
| 3 | 4 | 5 |
| 5 | 6 | 8 |
para calcular su A+ se procede de manera análoga:
Importancia
La propiedad 3 vista antes permite a partir de la matriz adjunta obtener la matriz inversa mediante el producto escalar:
A-1=|A|-1A+
Aunque se preferirá el método de Jordan debido a que para matrices de órdenes mayores que 3, éste tiene menos iteracciones y menor complejidad en los cálculos y la notación.
Véase también
Fuentes
- Colectivo de Autores. Álgebra lineal. Editorial Félix Varela, La Habana, 2003.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir, Moscú, 1988.
- Matriz invertible en Wikipedia.