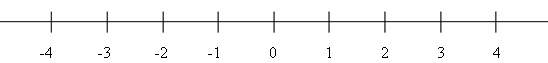Diferencia entre revisiones de «Números enteros»
(Etiqueta: nuestro-nuestra) |
(Etiqueta: nuestro-nuestra) |
||
| Línea 48: | Línea 48: | ||
Para describir la posición de cualquier punto sobre un plano, usamos ejes de coordenadas, de forma que cada punto tendrá dos coordenadas: una sobre el eje horizontal (eje x o eje de las abscisas) y la otra sobre el vertical (eje y o eje de las ordenadas). <br<br>Dichas coordenadas serán números enteros. <br>Por ejemplo, el punto A tiene -2 unidades de coordenada horizontal y 3 de coordenada vertical. El punto B tiene 3 unidades de coordenada horizontal y -3 unidades de coordenada vertical. | Para describir la posición de cualquier punto sobre un plano, usamos ejes de coordenadas, de forma que cada punto tendrá dos coordenadas: una sobre el eje horizontal (eje x o eje de las abscisas) y la otra sobre el vertical (eje y o eje de las ordenadas). <br<br>Dichas coordenadas serán números enteros. <br>Por ejemplo, el punto A tiene -2 unidades de coordenada horizontal y 3 de coordenada vertical. El punto B tiene 3 unidades de coordenada horizontal y -3 unidades de coordenada vertical. | ||
| − | [[Image:Ejes coordenados.jpg|center|341x289px|Ejes coordenados.jpg]] | + | [[Image:Ejes coordenados.jpg|center|341x289px|Ejes coordenados.jpg]] |
| − | == Orden de los números enteros == | + | == Orden de los números enteros == |
| − | Un número entero es mayor que otro (lo que se indica con el símbolo >) si está situado más a la derecha sobre la recta numérica. <br>Por ejemplo, 3 > -2; 3 > -1; -2 > -4: <br> [[Image:Orden1.jpg|center]]De la misma forma, un número entero es menor que otro (símbolo <) si está situado a la izquierda sobre la recta numérica. <br><br>Por ejemplo, -6 < 4; -3 < -1; -3 < 0; 3 < 6<br> | + | Un número entero es mayor que otro (lo que se indica con el símbolo >) si está situado más a la derecha sobre la recta numérica. <br>Por ejemplo, 3 > -2; 3 > -1; -2 > -4: <br> [[Image:Orden1.jpg|center|Orden1.jpg]]De la misma forma, un número entero es menor que otro (símbolo <) si está situado a la izquierda sobre la recta numérica. <br><br>Por ejemplo, -6 < 4; -3 < -1; -3 < 0; 3 < 6<br> |
| − | == [[Image: | + | [[Image:Orden2.jpg|center|Orden2.jpg]]<br> |
| + | |||
| + | == Suma de un entero positivo sobre la recta numérica<br> == | ||
| + | |||
| + | Para sumarle a cualquier número entero otro entero positivo, nos situamos sobre el punto que representa el primer sumando y avanzamos hacia la derecha tantas unidades como nos indique el segundo sumando.<br>Por ejemplo, para efectuar la suma -5 + 3: | ||
| + | |||
| + | #Nos situamos en el punto de la recta que representa – 5: | ||
| + | #[[Image:Suma 1.jpg|center]]Avanzamos desde ese punto tres unidades hacia la derecha:<br> | ||
| + | |||
| + | [[Image:Suma 2.jpg|center]]<br> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | == Ver también == | ||
*[[Ábaco|Ábaco]] | *[[Ábaco|Ábaco]] | ||
| Línea 69: | Línea 84: | ||
</div> | </div> | ||
[[Category:Teoría_elemental_de_los_números]] | [[Category:Teoría_elemental_de_los_números]] | ||
| + | |||
| + | <br> | ||
Revisión del 00:52 27 ene 2011
| ||||||
Números Enteros. Con los números naturales podemos contar todo cuanto nos rodea: un grupo de 5 estudiantes, una caravana de 10 autos, una bandada formada por 47 pájaros..., pero no manejamos el número 0, ni podemos representar situaciones como estas:
- Estamos a 5 grados bajo cero: - 5 º C.
- La ciudad está a 500 metros por debajo del nivel del mar: -500 m
- La mina está a 80 metros de profundidad: - 80 m.
En estos casos estamos usando números enteros negativos, números precedidos del signo menos (-).
Sumario
Número entero
Cualquier elemento del conjunto formado por los números naturales y sus opuestos. El conjunto de los números enteros se designa por Z:
Estos son:
- Los enteros positivos (o números naturales): +1, +2, +3, +4, +5...
- El 0, que no es ni positivo ni negativo.
- Los enteros negativos: -1, -2, -3, -4, -5...
Los números negativos satisfacen la necesidad de expresar la relatividad entre fenómenos que tienen lugar en nuestro entorno, tales como permiten contar nuevos tipos de cantidades (como los saldos deudores) y ordenar por encima o por debajo de un cierto elemento de referencia (las temperaturas superiores o inferiores a 0 grados, los pisos de un edificio por encima o por debajo de la entrada al mismo, incumplimientos de normas y planes de producción, retrasos en trayectorias que describe un móvil, …).
Tipos de enteros
- Si a, b y c son números enteros tales que a = bc, a es un múltiplo de b o de c, y b y c son divisores de a. Si c es distinto de ±1, entonces b se denomina divisor propio de a.
- Los enteros pares son los múltiplos de 2, incluyendo el 0, como -4, 0, 2 y 10;
- Un entero impar es aquél que no es par, por ejemplo, -5, 1, 3, 9.
- Un número perfecto es aquel entero positivo que es igual a la suma de todos sus divisores propios positivos (partes alícuotas); por ejemplo, 6 (que es igual a 1 + 2 + 3) y 28 (que es igual a 1 + 2 + 4 + 7 + 14) son números perfectos.
- Un entero positivo que no es perfecto se denomina imperfecto y puede ser deficiente o superante según que la suma de sus divisores propios positivos sea menor o mayor que él. Así, 9, cuyos divisores son 1 y 3, es deficiente, y 12, cuyos divisores son 1, 2, 3, 4 y 6, es superante.
Resumiendo:
- Todos los números enteros mayores que cero se consideran positivos, y sus opuestos, se consideran negativos.
- El cero no es positivo, ni negativo, luego el opuesto del cero es el propio cero.
- El conjunto formado por el cero y todos los números enteros positivos, se denomina conjunto de los números enteros no negativos.
- El conjunto formado por el cero y todos los números enteros negativos, se denomina conjunto de los números enteros no positivos.
- Los números opuestos están situados en la recta numérica simétricamente respecto al cero
- Los números enteros que solo se diferencian en el signo, se llaman opuestos, por ejemplo, 20 y -20 son números opuestos.
Representación de los números enteros sobre una recta
Se representan sobre una recta, llamada recta numérica, así:
El cero en mitad de la recta, los enteros negativos a la izquierda del cero y los enteros positivos a su derecha. Normalmente no escribimos el signo + que precede a los enteros positivos.
Representación de los números enteros sobre el plano
Para describir la posición de cualquier punto sobre un plano, usamos ejes de coordenadas, de forma que cada punto tendrá dos coordenadas: una sobre el eje horizontal (eje x o eje de las abscisas) y la otra sobre el vertical (eje y o eje de las ordenadas). <br
Dichas coordenadas serán números enteros.
Por ejemplo, el punto A tiene -2 unidades de coordenada horizontal y 3 de coordenada vertical. El punto B tiene 3 unidades de coordenada horizontal y -3 unidades de coordenada vertical.
Orden de los números enteros
Un número entero es mayor que otro (lo que se indica con el símbolo >) si está situado más a la derecha sobre la recta numérica.Por ejemplo, 3 > -2; 3 > -1; -2 > -4:
De la misma forma, un número entero es menor que otro (símbolo <) si está situado a la izquierda sobre la recta numérica. <br>
Por ejemplo, -6 < 4; -3 < -1; -3 < 0; 3 < 6
Suma de un entero positivo sobre la recta numérica
Para sumarle a cualquier número entero otro entero positivo, nos situamos sobre el punto que representa el primer sumando y avanzamos hacia la derecha tantas unidades como nos indique el segundo sumando.
Por ejemplo, para efectuar la suma -5 + 3:
- Nos situamos en el punto de la recta que representa – 5:
- Avanzamos desde ese punto tres unidades hacia la derecha:
Ver también
Fuentes
- Cuaderno complementario. Matemática 8vo grado
- Libro de texto. Matemática 7mo grado
- Rosell Franco, Sócrates. Aritmética, Volumen I, Editora Pedagógica. La Habana, 1966.