Diferencia entre revisiones de «Algoritmo de Thompson»
(Página creada con '{{Definición|nombre=Algoritmo de Thompson|imagen=noAFND.png|concepto=Algoritmo para obtener AFND-V a partir de expresiones regulares.}} <div align="justify"> '''Algoritmo de Th...') |
|||
| Línea 4: | Línea 4: | ||
==Definición== | ==Definición== | ||
| − | Sea una expresión regular ''E'' se recorre la misma según el orden de precedencia operacional (*, | + | Sea una expresión regular ''E'' se recorre la misma según el orden de precedencia operacional (*, ., |) y los agrupadores para obtener un AFND-V definido por su [[diagrama de estado]] según los pasos: |
# Se coloca el estado inicial ''Q0'':[[Archivo:AF_Estado_Inicio.gif|middle]]. | # Se coloca el estado inicial ''Q0'':[[Archivo:AF_Estado_Inicio.gif|middle]]. | ||
# Si la expresión admite la cadena vacía, ''Q0'' se indica como un estado final: [[Archivo:AF_Estado_Inicio_Final.gif|middle]] | # Si la expresión admite la cadena vacía, ''Q0'' se indica como un estado final: [[Archivo:AF_Estado_Inicio_Final.gif|middle]] | ||
| − | # | + | # Cada símbolo terminal se representa mediante una transición [[Archivo:AFD_Transicion.gif|middle]]. |
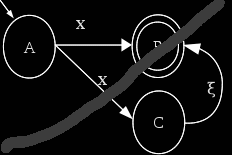
| − | # ''' | + | # '''Disjunción'''. Sea la expresión ''e<sub>1<sub>|e<sub>2<sub>'' el AFND-V equivalente toma la forma:[[Archivo:Thompson_Disjuncion.gif|middle]] donde ''T(e<sub>1<sub>)'' y ''T(e<sub>2<sub>)'' son los AFND-V resultantes de las expresiones ''e<sub>1<sub>'' y ''e<sub>2<sub>''respectivamente. |
| − | # ''' | + | # '''Concatenación (.)'''. Sea la expresión ''e<sub>1<sub>.e<sub>2<sub>'' o simplemente ''e<sub>1<sub>e<sub>2<sub>''el AFND-V equivalente toma la forma:[[Archivo:Thompson_Concatenacion.gif|middle]] donde ''T(e<sub>1<sub>)'' y ''T(e<sub>2<sub>)'' son los AFND-V resultantes de las expresiones ''e<sub>1<sub>'' y ''e<sub>2<sub>''. Tras la concatenación normalmente ''T(e<sub>1<sub>)'' pierde sus estados finales para dejar sólo los de ''T(e<sub>2<sub>)''. |
| − | # ''' | + | # '''Clausura (*)'''. Sea la expresión ''e<sub>1<sub>*'' el AFND-V equivalente toma la forma:[[Archivo:Thompson_Clausura.gif|middle]] donde ''T(e<sub>1<sub>)'' es el AFND-V resultante de las expresión ''e<sub>1<sub>''. |
| − | == | + | ==Véase también== |
* [[Expresión regular]]. | * [[Expresión regular]]. | ||
* [[Diagrama de estados]]. | * [[Diagrama de estados]]. | ||
Revisión del 17:33 30 nov 2013
| ||||||
Algoritmo de Thompson. Algoritmo que permite a partir de una expresión regular obtener un autómata finito no determinista con transiciones vacías (AFND-V) equivalente.
Definición
Sea una expresión regular E se recorre la misma según el orden de precedencia operacional (*, ., |) y los agrupadores para obtener un AFND-V definido por su diagrama de estado según los pasos:
- Se coloca el estado inicial Q0:
. - Si la expresión admite la cadena vacía, Q0 se indica como un estado final:
- Cada símbolo terminal se representa mediante una transición
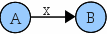. - Disjunción. Sea la expresión e1|e2 el AFND-V equivalente toma la forma:
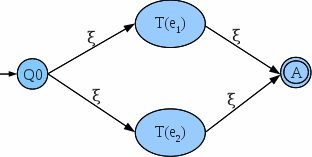donde T(e1) y T(e2) son los AFND-V resultantes de las expresiones e1 y e2respectivamente. - Concatenación (.). Sea la expresión e1.e2 o simplemente e1e2el AFND-V equivalente toma la forma:
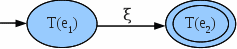donde T(e1) y T(e2) son los AFND-V resultantes de las expresiones e1 y e2. Tras la concatenación normalmente T(e1) pierde sus estados finales para dejar sólo los de T(e2). - Clausura (*). Sea la expresión e1* el AFND-V equivalente toma la forma:
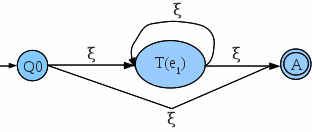donde T(e1) es el AFND-V resultante de las expresión e1.
Véase también
Fuentes
- Tanembaum, A. Compilers: Principles, Tecniques, and Tools. Tomo 1. ACM Press. 5ta Edición.
- Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente. Santiago de Cuba, 2000.
- Autómata finito en Wikipedia. Consultado el 25 de noviembre de 2013.
- Acevedo Martínez, Liesner; Osorio Ramírez, Karel. Manual de apoyo a la docencia. Técnicas de Compilación: Manual Práctico para estudiantes de Informática. Libro electrónico en PDF. UCI. La Habana, 2011.
- Algoritmo de Thompson en Wikipedia. Consultado el 30 de noviembre de 2013.
