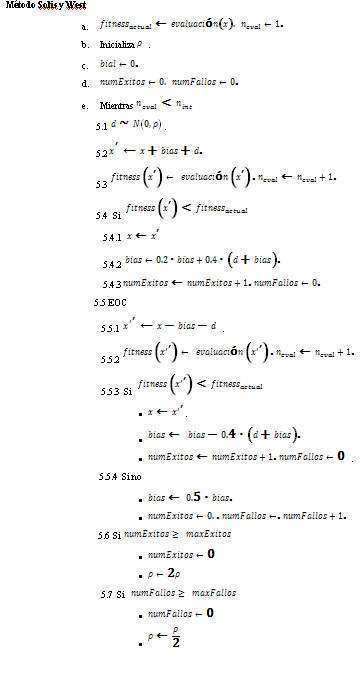Diferencia entre revisiones de «Método Solis Wets»
| Línea 1: | Línea 1: | ||
| − | |||
{{Definición | {{Definición | ||
|nombre= | |nombre= | ||
| Línea 6: | Línea 5: | ||
|tamaño= | |tamaño= | ||
|concepto= | |concepto= | ||
| − | Método de | + | Método de búsqueda local o meta-heurística de trayectoria simple. |
}} | }} | ||
<div align="justify"> | <div align="justify"> | ||
| − | + | '''Método Solis Wets.''' Método de búsqueda local o meta-heurística de trayectoria simple. Sigue un esquema de ascensión de colinas con un tamaño de salto adaptativo. Fue diseñado por F. J. Solís y R.J. Wets. En cada iteración se parte de una solución actual. Se genera un [[valor]] mediante una distribución normal con 0 de media y ρ de desviación estándar. La nueva solución se obtiene sumando dicho valor d junto con un valor que mantiene un cierto grado de "[[inercia]]" sobre los [[movimiento]]s anteriores. | |
| − | '''Método Solis Wets''' | + | |
| − | |||
==Caracterización== | ==Caracterización== | ||
Se caracteriza en varios aspectos: | Se caracteriza en varios aspectos: | ||
| − | * | + | * Las nuevas soluciones se obtienen mediante la [[suma]] de una [[variable]] de incremento (generada mediante una distribución normal N (0,ρ) y una variable. Esta variable permite mantener una [[inercia]] (orientando la búsqueda hacia direcciones exitosas en iteraciones anteriores). |
| − | * | + | * En cada paso se considera una dirección y si el resultado no es mejorado, se toma como nueva dirección de búsqueda, el sentido contrario a la dirección empleada hasta ese momento. |
| − | * | + | * Cuenta el [[número]] de éxitos (soluciones que mejoran a la actual) o fallos (soluciones peores que la actual) consecutivos. En función de unos [[valores]] máximos, el parámetro ρ es incrementado o decrementado, para aumentar o disminuir el espacio de búsqueda sobre la solución actual. |
| − | + | ||
[[Archivo:Método Solis y West.jpg]] | [[Archivo:Método Solis y West.jpg]] | ||
| − | + | ||
==Fuente== | ==Fuente== | ||
| − | * Solis, F. J. and R. J. West (1981). "Minimization by Random Search Techniques."Mathematical Operations Research. 6: 19–30. | + | * Solis, F. J. and R. J. West ([[1981]]). "Minimization by Random Search Techniques."Mathematical Operations Research. 6: 19–30. |
| − | |||
[[Category:Ciencias Aplicadas y Tecnologías]] | [[Category:Ciencias Aplicadas y Tecnologías]] | ||
Revisión del 16:39 7 feb 2014
| ||||
Método Solis Wets. Método de búsqueda local o meta-heurística de trayectoria simple. Sigue un esquema de ascensión de colinas con un tamaño de salto adaptativo. Fue diseñado por F. J. Solís y R.J. Wets. En cada iteración se parte de una solución actual. Se genera un valor mediante una distribución normal con 0 de media y ρ de desviación estándar. La nueva solución se obtiene sumando dicho valor d junto con un valor que mantiene un cierto grado de "inercia" sobre los movimientos anteriores.
Caracterización
Se caracteriza en varios aspectos:
- Las nuevas soluciones se obtienen mediante la suma de una variable de incremento (generada mediante una distribución normal N (0,ρ) y una variable. Esta variable permite mantener una inercia (orientando la búsqueda hacia direcciones exitosas en iteraciones anteriores).
- En cada paso se considera una dirección y si el resultado no es mejorado, se toma como nueva dirección de búsqueda, el sentido contrario a la dirección empleada hasta ese momento.
- Cuenta el número de éxitos (soluciones que mejoran a la actual) o fallos (soluciones peores que la actual) consecutivos. En función de unos valores máximos, el parámetro ρ es incrementado o decrementado, para aumentar o disminuir el espacio de búsqueda sobre la solución actual.
Fuente
- Solis, F. J. and R. J. West (1981). "Minimization by Random Search Techniques."Mathematical Operations Research. 6: 19–30.