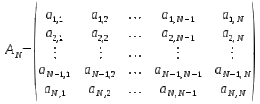Diferencia entre revisiones de «Matriz cuadrada»
(→Definiciones.) |
|||
| Línea 4: | Línea 4: | ||
'''Matriz cuadrada'''. Sea la [[Matriz]] de ''NxM'' filas y columnas respectivamente se dice que es cuadrada cuando ''N=M'', también se dice que es de orden ''N''. | '''Matriz cuadrada'''. Sea la [[Matriz]] de ''NxM'' filas y columnas respectivamente se dice que es cuadrada cuando ''N=M'', también se dice que es de orden ''N''. | ||
| − | == Definiciones | + | == Definiciones == |
Dada la matriz ''A'' de ''N'' filas y ''M'' columnas se dice que: | Dada la matriz ''A'' de ''N'' filas y ''M'' columnas se dice que: | ||
| Línea 17: | Línea 17: | ||
* ''A<sup>+</sup>'' es la [[matriz adjunta]] de ''A'', donde ''A<sup>+</sup>'' es una matriz cuadrada de mismo orden de ''A'' y es la transpuesta de una matriz cuyos elementos son los complementos algebraicos de las correspondientes celdas de ''A''. | * ''A<sup>+</sup>'' es la [[matriz adjunta]] de ''A'', donde ''A<sup>+</sup>'' es una matriz cuadrada de mismo orden de ''A'' y es la transpuesta de una matriz cuyos elementos son los complementos algebraicos de las correspondientes celdas de ''A''. | ||
| − | == Ejemplo | + | == Ejemplo == |
Dada la relación: | Dada la relación: | ||
| Línea 58: | Línea 58: | ||
* [[Matriz de adyacencia]] | * [[Matriz de adyacencia]] | ||
| − | == Fuentes | + | == Fuentes == |
* K. Ribnikov. Análisis Combinatorio. Editorial Mir Moscú. 1988. | * K. Ribnikov. Análisis Combinatorio. Editorial Mir Moscú. 1988. | ||
[[Category:Matemáticas]][[Category:Álgebra]] | [[Category:Matemáticas]][[Category:Álgebra]] | ||
Revisión del 13:36 19 ene 2017
| ||||||
Matriz cuadrada. Sea la Matriz de NxM filas y columnas respectivamente se dice que es cuadrada cuando N=M, también se dice que es de orden N.
Definiciones
Dada la matriz A de N filas y M columnas se dice que:
- A es cuadrada si y sólo si N=M.
- A de orden N si es cuadrada con N filas.
- Las operaciones A+B (suma matricial), AB (producto matricial) están definidas y producen una nueva matriz cuadrada de orden N siempre que B sea también cuadrada de orden N.
- |A|=n (determinante de A) donde n es un cardinal según el dominio de definición de A (se asumen los reales por defecto).
- A es singular ssi '|A|=0'.
- Si las celdas Ai,i=1 (diagonal principal) mientras Ai,j=0 siempre que i≠j se dice que A es la matriz identidad de orden N ó IN.
- Si las celdas Ai,i≠0 (diagonal principal) mientras Ai,j=0 siempre que i≠j se dice que A es una matriz diagonal.
- A-1 es la llamada matriz inversa de A tal que A-1A=AA-1=IN y existe siempre que |A|≠0.
- A+ es la matriz adjunta de A, donde A+ es una matriz cuadrada de mismo orden de A y es la transpuesta de una matriz cuyos elementos son los complementos algebraicos de las correspondientes celdas de A.
Ejemplo
Dada la relación:
- G=<{0, 1, 2, 3, 4, 5, 6, 7, 8}, ((0, 3), (0, 4), (0, 5), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 6), (3, 7), (8, 3), (4, 6), (4, 7), (8, 4), (5, 6), (5, 7), (8, 5))>.
la matriz de adyacencia asociada al grafo sería la matriz cuadrada:
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 5 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
Véase también
Fuentes
- K. Ribnikov. Análisis Combinatorio. Editorial Mir Moscú. 1988.