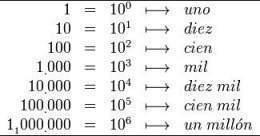Sistema decimal

Sistema decimal Concepto: Es un sistema de numeración posicional en el que las cantidades se representan utilizando como base el número diez.

Sistema decimal. Este sistema fue desarrollado por los hindúes, posteriormente lo introducen los árabes en Europa, donde recibe el nombre de sistema de numeración decimal o arábigo.

Función

Es un sistema de numeración posicional en el que las cantidades se representan utilizando como base el número diez, por lo que se compone de diez cifras diferentes: cero (0); uno (1); dos(2); tres (3); cuatro (4); cinco (5); seis (6); siete (7); ocho (8) y nueve (9). Este conjunto de símbolos se denomina números árabes, y es de origen hindú.

Excepto en ciertas culturas, es el sistema de posición usado habitualmente en todo el mundo y en todas las áreas que requieren de un sistemade numeración. Sin embargo hay ciertas técnicas, como por ejemplo en la informática, donde se utilizan sistemas de numeración adaptados al método de trabajo como el binario o el hexadecimal. También pueden existir en algunos idiomas vestigios del uso de otros sistemas de numeración, como el quinario, el duodecimal y el vigesimal. Por ejemplo, cuando se cuentan artículos por docenas, o cuando se emplean palabras especiales para designar ciertos números; en francés, por ejemplo, el número 80 se expresa «quatre-vingt», «cuatro veintenas», en español.

Según los antropólogos, el origen del sistema decimal está en los diez dedos que tenemos los humanos en las manos, los cuales siempre nos han servido de base para contar.

El sistema decimal es un sistema de numeración posicional, por lo que el valor del dígito depende de su posición dentro del número.

Así: 347 = 3 x 100 + 4 x 10 + 7 x 1 = 3 x 10^2 + 4 x 10^1 + 7 x 10^0

Los números decimales se pueden representar en la recta real.

Sistema decimal en el idioma español

Para el separador decimal, la Real Academia Española aconseja para separar la parte entera de la decimal debe usarse la coma, según establece la normativa internacional: El valor de π es 3,1416. No obstante, también se admite el uso anglosajón del punto, extendido en algunos países americanos.

También se suele utilizar la coma alta ( ' ) como separador.

En número π seria 3'1416.

Como separador de millares, lo más usual en español es utilizar un punto, un subíndice 1 como separador de millones, un subíndice 2 como separador de billones, 3 de trillones, etc.

No obstante la RAE aconseja la separación mediante espacios para que no haya confusión con los decimales, agrupándolos cada tres dígitos (exceptuando números de 4 cifras): Al escribir números de más de cuatro cifras, se agruparán estas de tres en tres, empezando por la derecha, y separando los grupos por espacios en blanco: 8 327 451 (y no por puntos o comas, como, dependiendo de las zonas, se hacía hasta ahora: 8.327.451; 8,327,451). Los números de cuatro cifras se escriben sin espacios de separación: 2458 (no 2 458). En ningún caso deben repartirse en líneas diferentes las cifras que componen un número: 8 327 / 451.

Fracciones

Algunas fracciones muy simples, como 1/3, tienen infinitas cifras decimales. Por eso, algunos han propuesto la adopción del sistema duodecimal, en el que 1/3 tiene una representación más sencilla.

• 1/2 = 0,5

  1/3 = 0,3333...

  1/4 = 0,25

  1/5 = 0,2

  1/6 = 0,1666...

  1/7 = 0,142857142857...

  1/8 = 0,125

  1/9 = 0,1111...

Búsqueda de números primos

En base 10, un número primo sólo puede acabar en 1, 3, 7 o 9.

Las 7 posibilidades restantes generan siempre números compuestos:

• Los acabados en 2, 4, 6, 8 y 0 son múltiplos de 2,
• Los acabados en 5 y 0 son múltiplos de 5.

Sistema negadecimal

En este caso, la base del sistema es el número negativo -10.. Se presentan ejemplos:

• Escriíbase -1 en base negadecimal. -1= -10+9 = 1(-10) + 9= (19)_-10
• Poner 10 en base negadecimal. 10= (-1)(-10)= (9-10)(-10)=9(-10) +(-10)²=(-10)²+1(-10)¹+0(-10)₀= (190)_-10

Indicaciones

• Las cifras usables son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
• Órdenes: negaünidades, (-10)⁰; negadecenas, (-10)¹; negacentenas, (-10)²; negamillares, (-10)³, así sucesivamente.

Fuentes

• Sócrates Rosell, F. Volumen I(Segunda Edición). Editorial Pedagógica.

Referencias