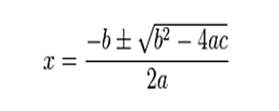Ecuación de segundo grado

Ecuación de Segundo Grado Concepto: Toda ecuación de la forma <math>ax^2 + b x + c = 0</math> (a, b, c Є R, a ≠ 0)

Ecuación de segundo grado. Toda ecuación de la forma ax²+bx+c=0 (a, b, c Є R, a ≠ 0) se denomina ecuación de segundo grado o cuadrática. La ecuación es completa si los tres coeficientes (a, b y c) son distintos de cero. Si algunos de los coeficientes b y c es igual a 0, entonces la ecuación es incompleta .

Resolución

Existen varias técnicas o métodos para calcular las raíces (soluciones) de una ecuación de segundo grado. La técnica más empleada es la aplicación de la fórmula cuadrática.

Fórmula cuadrática

Las soluciones de una ecuación de segundo grado en la forma general ax² + bx + c = 0 vienen dadas por la fórmula cuadrática:

Al radicando de fórmula, D = b² - 4·a·c, se le denomina discriminante de la ecuación. El número (y tipo) de soluciones queda determinado por el signo del discriminante.

Tipos de soluciones

Las ecuaciones de segundo grado tienen siempre dos soluciones complejas (que a su vez pueden ser reales). En el caso de la ecuación con coeficientes reales, pueden darse las siguientes tres situaciones

Una solución

Si el discriminante es 0, D = 0, entonces las dos soluciones son reales e iguales, por lo que puede decirse que existe una única solución (de multiplicidad doble).

Ejemplos:

• La ecuación x² + 2x + 1 = 0 tiene una única solución x = -1.
• La ecuación x² -2x +1 = 0 tiene una única solución x = 1.

Dos soluciones (reales)

Si el discriminante es positivo, D > 0, entonces existen dos soluciones reales distintas (de multiplicidad 1).

Ejemplos:

• La ecuación incompleta x² - 1 = 0 tiene dos soluciones reales: x=1 y x = -1. Su discriminante es D = 4 > 0.
• La ecuación completa x² + x - 2 = 0 tiene dos soluciones reales: x=1 y x = -2. Su discriminante es D = 9 > 0.

Dos soluciones no reales

Si el discriminante es negativo, D < 0, entonces las dos soluciones son números complejos conjugados. Esto se debe al hecho de que la raíz cuadrada de un número negativo es un número complejo. Es común decir que la ecuación no tiene soluciones, refiriéndose a que la ecuación no tiene soluciones reales. En el caso de que los coeficientes sean números complejos, existen exactamente dos raíces complejas no conjugadas (habrá que hallar raíz de un número complejo).

Ejemplos:

• La ecuación incompleta x² + 1 = 0 tiene dos soluciones complejas: x = i y x = -i. Su discriminante es D = -4 < 0.
• La ecuación completa "x² - 2x + 5 = 0" tiene dos soluciones complejas: x = 1 + 2i y x = 1- 2i. Su discriminante es D = -16 < 0.

Referencias

Algoritmo de resolución

Para resolver una ecuación cuadrática después de expresada ax2 + bx + c = 0 (a ≠ 0), puedes utilizar el algoritmo siguiente: 1. Identifica los cocientes a, b y c 2. Sustituye los valores en la formula del discriminante D = b2 - 4ac. 3. Si D < 0, entonces no posee soluciones reales y finaliza. 4. Si D = 0, entonces posee una sola solución x = - b/2ª

Ejemplos

Son ecuaciones de segundo grado los siguientes ejemplos

• x² - 2x + 35 = 0
• 4x² – 9 = 0
• 2x² = 0

Hay ecuaciones que mediante transformaciones algebraicas se transforman en ecuaciones cuadráticas, por ejemplo

• x² = x + 3
• 2x² = 8
• (x - 2)(x + 1) = 10

Fuente

• Libro de texto Matemática 9no grado, Editorial Pueblo y Educación, 2001