Proporcionalidad
Proporcionalidad. Muchas veces en la práctica se nos presentan situaciones en las que el valor o cantidad de una magnitud depende del valor de otra. El factor constante de proporcionalidad puede utilizarse para expresar las relaciones entre las magnitudes.
| ||||||
Sumario
Reseña histórica
Las matemáticas son el estudio de las relaciones entre cantidades, magnitudes y propiedades, y de las operaciones lógicas utilizadas para deducir cantidades, magnitudes y propiedades desconocidas. A finales del siglo V a.C., descubrieron que no existía una unidad de longitud capaz de medir el lado y la diagonal de un cuadrado, puesto que una de las dos cantidades es inconmensurable, es decir, no existen dos números naturales cuyo cociente sea igual a la proporción entre el lado y la diagonal. Pero como los griegos sólo utilizaban los números naturales, no pudieron expresar numéricamente dicho cociente, ya que es un número irracional.
Proporcionalidad directa
Dos magnitudes son directamente proporcionales cuando al aumentar una, aumenta la otra en la misma proporción .
Si un metro de tela tiene un precio de $10, el costo de un corte de tela depende del número de metros que tenga de largo. A mayor número de metros de tela, mayor será el costo de la misma.
Esta relación la puedes apreciar en la siguiente tabla:
Observa que:
10=10 x 1 ; 20=10 x 2 ; 25=10 x 2,5 ; ... ... ... 100=10 x 10.
O sea que: el costo del corte de tela (en pesos) se obtiene multiplicando la longitud del corte (en metros) por el precio de un metro que es de $10.
Cuando dos magnitudes están relacionadas de modos que los
valores de una de ellas se obtienen multiplicando por un mismo
número los valores correspondientes en la otra, se dice que
son directamente proporcionales.
Podemos decir entonces que el costo de una tela es directamente proporcional a la longitud del corte. El número por el que se multiplica se llama factor de proporcionalidad. En este caso es 10 ese factor, que es el precio de 1 m de tela.
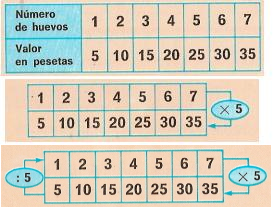
En la tabla siguiente se muestra otra correspondencia de proporcionalidad directa:
Observa que, cuando aumenta el número de panes aumenta el costo, y que las razones entre dos cantidades y sus correspondientes siempre son iguales. Por ejemplo:
En una proporcionalidad directa, dos cantidades cuales
quiera de una magnitud y sus correspondientes en la otra,
forman una proporción.
En este ejemplo el factor de proporcionalidad es 5, es el número por el cual se multiplica cada cantidad de panes para obtener su costo. Observa que el factor de proporcionalidad es el valor correspondiente al 1 y lo puedes obtener dividiendo cualquier cantidad de la segunda magnitud entre la cantidad al la cual corresponde en la primera.
Por ejemplo: 5 : 1 = 5 ; 10 : 2 = 5 ; 55 : 11 = 5 .
Si representas esta correspondencia en un sistema de coordenadas, puedes comprobar que los puntos que se obtienen al representar cada par de valores correspondientes están sobre una misma recta.
Existen ejemplos que conoces de la práctica, que son magnitudes directamente proporcionales:
- El costo y la cantidad de artículos, si se paga por unidad.
- El costo y el peso de artículos, si se paga por peso.
- El espacio recorrido y el tiempo de demora, si la velocidad es constante.
- El tiempo de trabajo y la obra producida, si el número de obreros es constante.
- El número de obreros y la obra producida, si el tiempo de trabajo es constante.
El conocer estos ejemplos te permitirá resolver con facilidad problemas que se te pueden presentar con frecuencia.
Proporcionalidad inversa
Enlaces externos
Fuentes
- Libro de texto de Matemática 6to grado. Editorial Pueblo y Educación, 1989.
- Profesorenlinea
- Thatquiz
- Todosloscomo
- PNTIC
- Lubrin