Diferencia entre revisiones de «Algoritmo de Dijkstra»
(Etiqueta: nuestro-nuestra) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| Línea 4: | Línea 4: | ||
|tamaño= | |tamaño= | ||
|concepto= El algoritmo de Dijkstra, también llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un grafo con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959. | |concepto= El algoritmo de Dijkstra, también llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un grafo con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959. | ||
| − | }} | + | }} |
'''Algoritmo de Dijkstra.''' También llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un [[grafo]] con pesos en cada arista. Su nombre se refiere a [[Edsger Dijkstra]], quien lo describió por primera vez en [[1959]]. | '''Algoritmo de Dijkstra.''' También llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un [[grafo]] con pesos en cada arista. Su nombre se refiere a [[Edsger Dijkstra]], quien lo describió por primera vez en [[1959]]. | ||
última versión al 15:09 20 jun 2019
Algoritmo de Dijkstra. También llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un grafo con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959.
Sumario
Aplicaciones
En múltiples aplicaciones donde se aplican los grafos, es necesario conocer el camino de menor costo entre dos vértices dados:
- Distribución de productos a una red de establecimientos comerciales.
- Distribución de correos postales.
- Sea G = (V, A) un grafo dirigido ponderado.
El problema del camino más corto de un vértice a otro consiste en determinar el camino de menor costo, desde un vértice u a otro vértice v. El costo de un camino es la suma de los costos (pesos) de los arcos que lo conforman.
Características del algoritmo
- Es un algoritmo greddy.
- Trabaja por etapas, y toma en cada etapa la mejor solución sin considerar consecuencias futuras.
- El óptimo encontrado en una etapa puede modificarse posteriormente si surge una solución mejor.
Pasos del algoritmo
Algoritmo 24.1: Algoritmo de Dijkstra. Inicialización.
- Sea V un conjunto de vértices de un grafo.
- Sea C una matriz de costos de las aristas del grafo, donde en C[u,v] se almacena el costo de la arista entre u y v.
- Sea S un conjunto que contendrá los vértices para los cuales ya se tiene determinado el camino mínimo.
- Sea D un arreglo unidimensional tal que D[v] es el costo del camino mínimo del vértice origen al vértice v.
- Sea P un arreglo unidimensional tal que P[v] es el vértice predecesor de v en el camino mínimo que se tiene construido.
- Sea vinicial el vértice origen. Recordar que el Algoritmo Dijkstra determina los caminos mínimos que existen partiendo de un vértice origen al resto de los vértices.
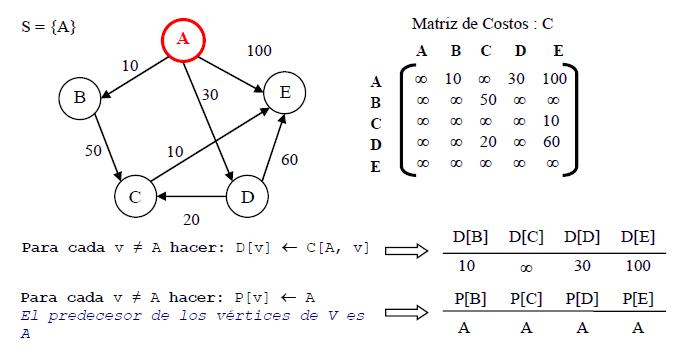
Paso 1. S ← {vinicial} //Inicialmente S contendrá el vértice //origen
Paso 2. Para cada v∈V, v ≠ vinicial, hacer
2.1. D[v] ← C[vinicial, v] //Inicialmente el costo del //camino mínimo de vinicial a v es lo contenido en //la matriz de costos
2.2. P[v] ← vinicial //Inicialmente, el //predecesor de v en el camino mínimo construido //hasta el momento es vinicial
Paso 3. Mientras (V – S ≠ ∅) hacer //Mientras existan vértices para //los cuales no se ha determinado el //camino mínimo
3.1. Elegir un vértice w∈(V-S) tal que D[w] sea el mínimo.
3.2. S ← S ∪ {w} //Se agrega w al conjunto S, pues ya se //tiene el camino mínimo hacia w
3.3. Para cada v∈(V-S) hacer
3.3.1. D[v] ← min(D[v],D[w]+C[w,v]) //Se escoge, entre //el camino mínimo hacia v que se tiene //hasta el momento, y el camino hacia v //pasando por w mediante su camino mínimo, //el de menor costo.
3.3.2. Si min(D[v],D[w]+C[w,v]) = D[w]+C[w,v] entonces P[v] ← w //Si se escoge ir por w entonces //el predecesor de v por el momento es w
Paso 4. Fin
Ejecución de algoritmo
- Paso 1: Inicialización
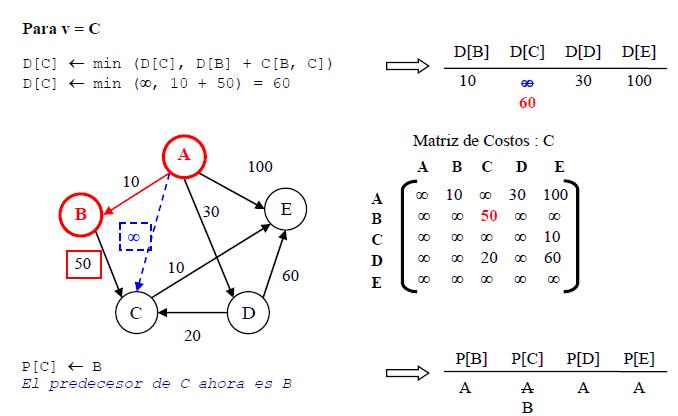
- Paso 2: Elegir un vértice w ∈ V - {A} tal que D[w] sea mínimo, y agregar w al conjunto solución S
- Paso 3: cada v ∈ {C, D, E} hacer D[v] ← min( D[v], D[w]+C[w, v] )
- Paso 4: Elegir un vértice w ∈ V - {A, B} tal que D[w] sea mínimo, y agregar w al conjunto solución S.
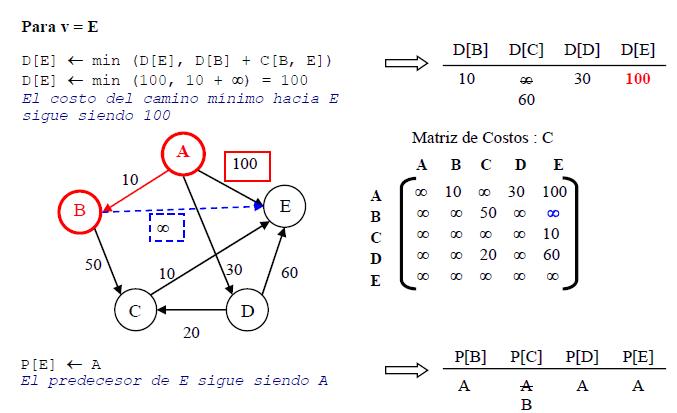
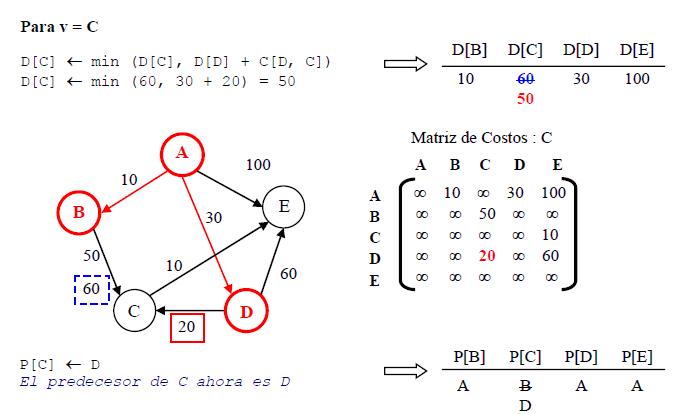
- Paso 5: Para cada v ∈ {C, E} hacer D[v] ← min( D[v], D[w]+C[w, v]
- Paso 6: Elegir un vértice w ∈ V - {A, B, D} tal que D[w] sea mínimo, y agregar w al conjunto solución S.
- Paso 7: Para cada v ∈ { E} hacer D[v] ← min( D[v], D[w]+C[w, v]
- Paso 8: Elegir un vértice w ∈ V - {A, B, D, C} tal que D[w] sea mínimo, y agregar w al conjunto solución S.
Final del Proceso de Ejecución
Luego del paso 8 tenemos la siguiente situación:
- El conjunto de vértices V = {A, B, C, D, E}
- El conjunto de vértices para los que ya se determinó el camino mínimo S = {A, B, D, C, E}
Por lo que como V-S=Ø se termina el algoritmo, pues para cada nodo del grafo se ha determinado cuál es su camino mínimo. Como resultado de la ejecución del algoritmo tenemos:
D[B] D[C] D[D] D[E] P[B] P[C] P[D] P[E]
10 50 30 60 A D A C
Al finalizar la ejecución del algoritmo Dijkstra, en el arreglo D quedan almacenados los costos de los caminos mínimos que parten del vértice origen al resto de los vértices. Por tanto, en nuestro ejemplo, el camino mínimo de A hacia B tiene costo 10, el camino mínimo de A hacia C tiene costo 50, el camino mínimo de A hacia D tiene costo 30 y el camino mínimo de A hacia E tiene costo 60.
Veamos cómo se pueden obtener los caminos mínimos a partir del arreglo de predecesores. Los caminos se reconstruyen partiendo del vértice destino hasta llegar al vértice origen.
CaminoMínimo (A, B) = AB ya que P[B]=A CaminoMínimo (A, C) = ADC ya que P[C]=D y P[D]=A CaminoMínimo (A, D) = AD ya que P[D]=A CaminoMínimo (A, E) = ADCE ya que P[E]=C, P[C]=D y P[D]=A
Finalmente, el camino mínimo que incluye todos los vértices del grafo es ADCE.
Pseudocódigo
Cola de prioridad
DIJKSTRA (Grafo G, nodo_fuente s)
para u ∈ V[G] hacer
distancia[u] = INFINITO
padre[u] = NULL
distancia[s] = 0
adicionar (cola, (s,distancia[s]))
mientras que cola no es vacía hacer
u = extraer_minimo(cola)
para todos v ∈ adyacencia[u] hacer
si distancia[v] > distancia[u] + peso (u, v) hacer
distancia[v] = distancia[u] + peso (u, v)
padre[v] = u
adicionar(cola,(v,distancia[v]))
Sin cola de prioridad
función Dijkstra (Grafo G, nodo_salida s)
//Usaremos un vector para guardar las distancias del nodo salida al resto entero distancia[n]
//Inicializamos el vector con distancias iniciales booleano visto[n]
//vector de boleanos para controlar los vertices de los que ya tenemos la distancia mínima
para cada w ∈ V[G] hacer
Si (no existe arista entre s y w) entonces
distancia[w] = Infinito //puedes marcar la casilla con un -1 por ejemplo
Si_no
distancia[w] = peso (s, w)
fin si
fin para
distancia[s] = 0
visto[s] = cierto
//n es el número de vertices que tiene el Grafo
mientras que (no_esten_vistos_todos) hacer
vertice = coger_el_minimo_del_vector distancia y que no este visto;
visto[vertice] = cierto;
para cada w ∈ sucesores (G, vertice) hacer
si distancia[w]>distancia[vertice]+peso (vertice, w) entonces
distancia[w] = distancia[vertice]+peso (vertice, w)
fin si
fin para
fin mientras
fin función
Enlaces externos
- Presentación del Algoritmo de Dijkstra
- Applets en Java para probar el algoritmo de Dijkstra (Inglés)
- Graph módulo Perl en CPAN
- Bio::Coordinate::Graph módulo Perl en CPAN que implementa el algoritmo de Dijkstra
- Video Tutorial en VideoPractico.com de Dijkstra
- giswiki.net Algoritmo de Dijkstra en lenguajes como PHP, Actionscript y otros