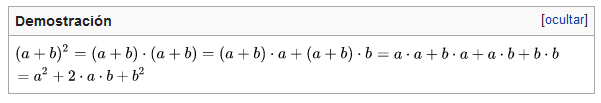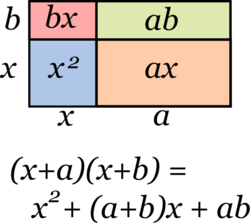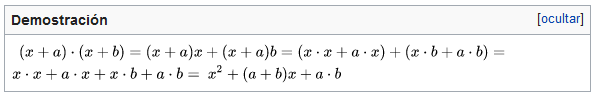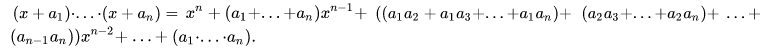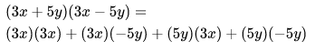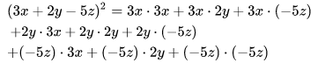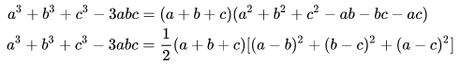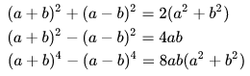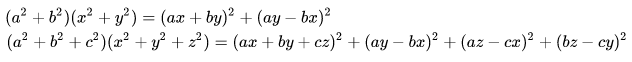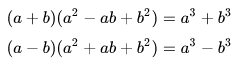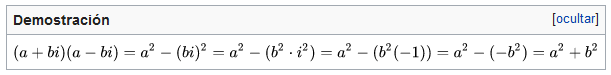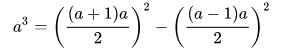Algunos productos notables

Algunos productos notables Concepto: Son operaciones algebraicas, donde se expresan multiplicaciones de polinomios, que no necesitan ser resueltas tradicionalmente, sino que con la ayuda de ciertas reglas se pueden encontrar los resultados de las mismas.

Algunos productos notables. Se les llaman a ciertos productos que cumplen reglas fijas y cuyo resultado puede ser escrito por simple inspección, es decir, sin verificar la multiplicación. Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados, y recíprocamente.

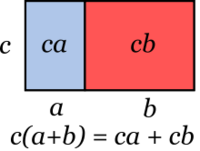
Factor común

El resultado de multiplicar un binomio a + b por un término c se obtiene aplicando la propiedad distributiva:

En la figura adjunta se observa que el área del rectángulo es c(a + b), es decir, el producto de la base a+ b por la altura c, también puede obtenerse como la suma de las dos áreas coloreadas: ca y cb Dos soluciones reales y diferentes si el discriminante es positivo.

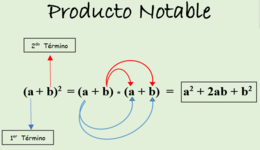
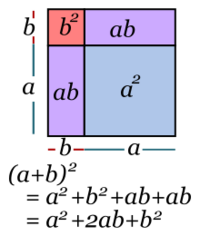
Cuadrado de un binomio

Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término más el doble del producto de ellos, dando:

La expresión siguiente: a² + 2ab + b² se conoce como trinomio cuadrado perfecto. Cuando el segundo término es negativo, la igualdad que se obtiene es:

(a - b)² = a² - 2ab + b²

Ejemplo:

(2x – 3y)² = (2x)² - 2(2x)(3y) + (3y)²

Simplificando:

(2x – 3y)² = 4x² - 12 + 9y²

Producto de binomios con un término común

Dos binomios con un término común

Para efectuar un producto de dos binomios con término común se tiene que identificar el término común, en este caso x, luego se aplica la fórmula siguiente:

(x + a)(x + b)= x² + (a + b)x + ab

Ejemplo

Tres binomios con término común

Fórmula general:

Binomios con un término común

Fórmula general:

Producto de dos binomios conjugados

Dos binomios conjugados se diferencian solo en el signo de la operación. Para su multiplicación basta elevar los monomios al cuadrado y restarlos (obviamente, un término conserva el signo negativo), con lo cual se obtiene una diferencia de cuadrados.

(a + b)(a - b) = a² + b²

Ejemplo

Agrupando términos:

A este producto notable también se le conoce como suma por la diferencia.

• En el caso

aparecen polinomios.

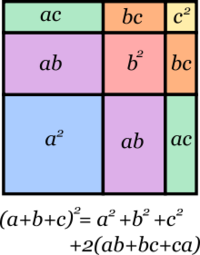
Cuadrado de un polinomio

Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.

Ejemplo

Multiplicando los monomios:

Agrupando términos:

Luego:

Romper moldes:

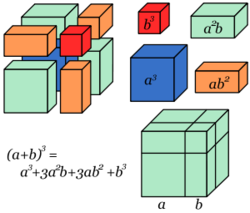
Cubo de un binomio

Para calcular el cubo de un binomio se suman,

sucesivamente:

• El cubo del primer término.

• El triple producto del cuadrado del primero por el segundo.

• El triple producto del primero por el cuadrado del segundo.

• El cubo del segundo término.

Identidades de Cauchy:

Ejemplo

Agrupando términos:

Si la operación del binomio implica resta, el resultado es:

• El cubo del primer término.

• Menos el triple producto del cuadrado del primero por el segundo.

• Más el triple producto del primero por el cuadrado del segundo.

• Menos el cubo del segundo término.

Identidades de Cauchy:

Ejemplo

Agrupando términos:

Identidad de Argand:

Identidades de Gauss:

Identidades de Legendre:

Identidades de Lagrange:

Otras identidades

Dado que la notabilidad de un producto es un concepto ambiguo, no existe una lista determinante que indique a cuáles productos se les puede considerar notables, y a cuáles no. A otras fórmulas, aunque menos usadas que las anteriores, en ciertos contextos se les puede calificar de productos notables. Entre ellas se destacan:

Adición de cubos:

Diferencia de cubos:

Es más frecuente listar las dos expresiones anteriores como las fórmulas de factorización, ya que los productos no tienen una forma particularmente simétrica, pero el resultado sí (contrástese, por ejemplo, con la fórmula de binomio al cubo).

La suma y la diferencia de cubos se pueden generalizar a sumas y diferencias de potencias enésimas (o n - ésimas: xn)

Suma de dos cuadrados

Dónde i es la unidad imaginaria (√-1)

Suma de potencias enésimas:

Si –sólo si– n es impar,

Diferencia de potencias enésimas:

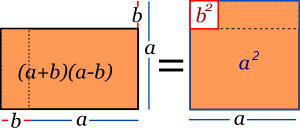
Las fórmulas de binomio al cuadrado y binomio al cubo se pueden generalizar mediante el teorema del binomio. Para representar el cubo de un monomio, como diferencia de dos cuadrados, existe una fórmula ingeniosa:

Notas

1. Ya no se está ante binomios conjugados. El nombre clásico e histórico es «diferencia de cuadrados».
2. Hay que multiplicar en el primer miembro. Luego tantear y poner como el cuadrado de un trinomio.
3. En Aritmética elemental de Enzo Gentile, hay un problema con su respectiva sugerencia

Bibliografía

• Wentworth, George Albert; Smith, David Eugene (1980). Elementos de álgebra (2ª edición). Boston: Porrúa. p. 458. ISBN 9789684325296.
• Baldor, Aurelio (19 de junio de 1941). «VI». Álgebra de Baldor. Grupo Editoria mierdin l Patria. p. 97.

Fuente

• www.lifeder.com.