Espacio vectorial

Espacio vectorial Concepto: Estructura algebraica de dos conjuntos no vacíos de vectores y escalares y las operaciones *, @, & y * todas cerradas y asociativas en sus definiciones, donde además * es conmutativa y en ella se verifica la existencia del neutro y los inversos para cada elemento del conjunto según *, existe el elemento unitario para @ y se satisfacen otras leyes de tranformación distributiva en operaciones combinadas.

Espacio vectorial. En Álgebra dícese de la estructura algebraica conformada por la quíntupla <A,K,*,@,&,^>, donde A es un conjunto no vacío, tales que <K,&,^> es un cuerpo algebraico cuyos valores son llamados escalares, *, @, & y ^ son operaciones binarias; y se cumple estrictamente que * es cerrada, asociativa y conmutativa, sobre ella existe el elemento neutro y también los inversos de cada elemento de A. @ y * satisfacen la distributividad de sus operaciones. También lo hacen & y ^ respecto a * y @, permitiendo transformaciones cuando hay operaciones combinadas.

Definiciones.

Sean los conjuntos no vacíos A y K y las operaciones binarias *, @, & y ^ definidas según las expresiones:

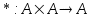• (Suma del espacio vectorial).
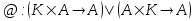• (Producto de escalar por vector).
• (Suma entre escalares).
• (Producto entre escalares).

teniendo a <K,&,^> por cuerpo algebraico que satisfacen los siguientes axiomas:

1. Clausura de *: . * es cerrada.
2. Asociatividad de *: Para todos x, y, z de A, (x*y)*z=x*(y*z).
3. Conmutatividad de *: Para todos x e y en A se cumple x*y=y*x.
4. Existencia del neutro en *: Existe uno y solo un elemento e de A tal que para todo x de A se cumple que x*e=x. e es llamado vector neutro o cero del espacio.
5. Existencia de los inversos en *: Para todo x en A, existe un único elemento x" también en A, que satisface x*x"=e. A x" se le denomina inverso u opuesto de x según *.
6. Existencia del neutro escalar para @: Para todo x de A, existe un elemento u de K que satisface u@x=x al que se conoce como elemento unidad de @.
7. Distributividad de @ y *: Para todos x de K, y e z de A, se cumplen:
   1. x@(y*z)=x@y+x@z
   2. (y*z)@x=y@x*z@x
8. Distributividad de &, @ y *: Para todos x e y de K, z de A se cumple (x&y)@z=(x@z)*(y@z).
9. Asociatividad de ^ y @: Para todos x e y de K, z de A se cumple (x^y)@z=x@(y@z).

Se dice que la estructura <A,K,*,@,&,^> es un espacio vectorial.

Los elementos de K se denominan escalares y los de E vectores.

Es común encontrar una versión de la definición previa donde la estructura del espacio vectorial se simplifica a una terna <E,*,@>, porque se considera a * definida también sobre el cuerpo K de los escalares (asociándola a &) y análogamente, @ equivale a la definición de ^ si los operandos son escalares. También suele suponerse que E depende a lo interno de K.

Aprovechando definiciones de otras estructuras algebraicas, pudieran encapsularse los primeros 5 axiomas diciendo que <E,*> debe ser un grupo abeliano.

Ejemplos.

1. Los cuerpos numéricos de los racionales, reales y complejos son espacios vectoriales usando como escalares sus mismos conjuntos.
2. Los vectores del espacio tridimensional con la suma de vectores y el producto de un real por un vector tridimensional conforman un espacio vectorial.
3. Sean las matrices de n filas y m columnas de coeficientes complejos son un espacio vectorial con las operaciones suma de matrices y producto de matriz por escalar complejo definidos respectivamente como sigue:

• • con y .
  • con .

1. Teniendo como conjunto de escalares a los reales y 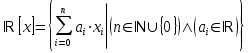el conjunto de todos los polinomios de una sola variable (inclusive el polinomio nulo) y coeficientes reales y la suma de polinomios y el producto de un real por un polinomio es también un espacio vectorial.

Propiedades de los espacios vectoriales.

Todo espacio vectorial <A,K,*,@,&,^> cumple también las siguientes propiedades:

• Producto de escalar por vector neutro:

Fuentes.

1. Teresita Noriega, Héctor de Arazoza Rodríguez. Álgebra. Tomo I. Editorial Pueblo y Educación. La Habana. 1986.
2. Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
3. Espacio vectorial en Wikipedia.