Diferencia entre revisiones de «Kn»
| Línea 26: | Línea 26: | ||
|- | |- | ||
| [[Image:K2.png|thumb|K<sub>2</sub>]] | | [[Image:K2.png|thumb|K<sub>2</sub>]] | ||
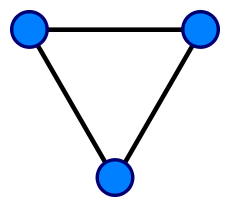
| − | | [[Image: | + | | [[Image:Grafok3.png|thumb|K<sub>3</sub>]] |
| − | | [[Image: | + | | [[Image:Grafok4.JPG|thumb|K<sub>4</sub>]] |
|- | |- | ||
| [[Image:K5.png|thumb|K<sub>5</sub>]] | | [[Image:K5.png|thumb|K<sub>5</sub>]] | ||
| Línea 33: | Línea 33: | ||
| [[Image:K20.png|thumb|K<sub>20</sub>]] | | [[Image:K20.png|thumb|K<sub>20</sub>]] | ||
|- | |- | ||
| − | | | + | | |
|} | |} | ||
Revisión del 10:50 11 sep 2013
| ||||||
Kn. Grafo completo simple de orden n.
Sumario
Características.
La familia de grafos Kn es la más simple de los grafos no orientados de orden equivalente pues no poseen ni multiaristas ni lazos pero logran, ya que son completos, la existencia de una arista entre cualquier par de nodos diferentes.
Esto produce caminos mínimos entre cualquier par de vértices.
Matriz de adyacencia.
La matriz de adyacencia en la familia Kn es fácil de reconocer pues todos sus elementos tienen valor 1, excepto los de la diagonal principal que son 0.
Luego, las potencias de dicha matriz siempre serán no nulas, identificando el hecho de que siempre existen caminos de cualquier orden entre los nodos.
Representación gráfica.
K2 son dos vértices unidos por una arista.
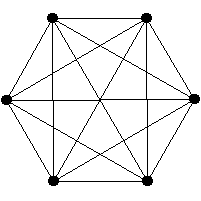
Los Kn suelen representarse como mismo los polígonos regulares de orden equivalente: se igualan los vértices de ambos y luego se trazan las aristas entre todos los pares de vértices.
Esta forma de representación permite obtener figuras conocidas como el triángulo equilátero; las estrella de 5 puntas dentro del pentágono (visto en textos antiguos asociados a la magia y la alquimia); el hexágono con 2 triángulos equiláteros inscritos inversos entre sí y otras que presentan gran armonía y complejidad visual.
Veáse también.
Fuentes.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir Moscú. 1988.