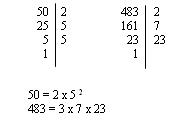Máximo común divisor

Máximo común divisor Concepto: El mayor de los divisores comunes de varios números

Máximo Común Divisor. Procedimiento matemático utilizado para resolver situaciones como la siguiente:

A un campamento de pioneros van 30 alumnos, de ellos 12 son niñas y 18 son niños, al llegar la noches estos deben acampar en cabañas. ¿De cuántas plazas, como máximo, debe ser cada cabaña para que cada una de ellas esté ocupada solo por chicos o solo por chicas?

Máximo común divisor

Máximo común divisor, de dos o más números naturales, es el mayor de sus divisores comunes.
Ejemplo: el mayor número que es divisor común de 18, 24 y 30 es 6; luego 6 es el máximo común divisor de 18, 24 y 30.
El máximo común divisor de varios números a, b, c, se designa abreviadamente así: m.c.d. (a, b, c). o también M.C.D. (a, b, c)
Para obtener el máximo común divisor de vario números naturales, existen varios métodos:

Métodos para hallar el m.c.d.

1- De acuerdo con la definición
El m.c.d. de varios números puede hallarse, de acuerdo con la definición, determinando todos los divisores, simples y compuestos, de cada uno de ellos y buscando después, entre esos divisores, cuáles son los comunes a todos los números dados. El mayor de esos divisores será el m.c.d.
Ejemplo:
a) Hallar el m.c.d. de 18, 24 y 42
Divisores de 18: 1, 2, 3, 6, 9, 18
Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24
Divisores de 42: 1, 2, 3, 6, 7, 14, 21, 42
Los divisores comunes de 18, 24 y 42 son: 1, 2, 3 y 6. El mayor es 6.
Luego el m.c.d. (18, 24, 42) = 6
Este método contribuye a aclarar el concepto de m.c.d., pero no es un método práctico, sumamente laborioso.

2- Por inspección
Se ve sucesivamente si el menor de esos números, o su mitad, o su tercera, o su cuarta, etc. (si las tiene) es divisor de los otros números dados. El primero que lo sea es el m.c.d. de todos ellos.
En cualquier caso en que un número divida a otro, el primero, el divisor, es el m.c.d. de los dos
Ejemplo:
a) Hallar el m.c.d. de 6, 18 y 24
Probamos el menor, 6 y como vemos que los otros dos son divisibles por él, el m.c.d. es 6
b) Hallar el m.c.d. de 10, 15, 45 y 90
El menor es 10, no divide a los otros. Probamos con su mitad, que es 5, y como si los divide, 5 es el m.c.d. de 10, 15, 45 y 90.
c) Hallar el m.c.d. de 6, 8 y 30
El menor es 6, no divide a los otros dos, su mitad es 3, tampoco; su tercera, 2, si los divide: por lo tanto, 2 es el m.c.d. de 6, 8 y 30.
En este método las operaciones son sencillas y se hacen mentalmente por lo que se sugiere cuando se trata de números pequeños.

3- Por descomposición en factores
Se descomponen los números dados en factores primos, se toman los factores comunes a todos ellos con el menor exponente que presenten en sus respectivas descomposiciones. El producto de esos factores será el m.c.d de los números dados.
Este método es el mejor siempre que no haya grandes dificultades para descomponer los números dados en sus factores primos.
Ejemplo:
a) Hallar el m.c.d de 180, 240 y 1400
Descomponemos los números en factores primos

Expresamos los números como productos, si algunos de los factores se repiten lo escribimos como potencia.
        180 = 22 x 32 x 5
        240 = 24 x 3 x 5
        1400 = 23 x 52 x 7
Analizamos cada factor y observamos si están en las tres descomposiciones, de estar lo tomamos con el menor exponente, en este caso el 2 y 5 está en las tres descomposiciones, tomamos el 2 con exponente 2 (22) y el 5 con exponente 1
Luego: m.c.d (180, 240, 1400) = 22 x 5 = 4 x 5 = 20

b) Hallar el m.c.d. de 50, 100 y 483

Prescindiendo del 100 por se múltiplo de 50, resulta:

Como no hay ningún factor común el m.c.d. de 50, 100 y 483 es 1, pues sabemos que el 1 es divisor de todos los números. Esto sucede cuando los números dados son primos entre sí

4- Por divisiones sucesivas. (Hay que distinguir dos casos)

1- Si se trata de dos números: se divide el mayor por el menor, este por el primer resto, éste por el segundo, y así sucesivamente hasta llegar a una división exacta. El último divisor empleado será el m.c.d. de esos números.
Si al dividir el mayor entre el menor la división fuera exacta, el menor sería el m.c.d.
Ejemplo.
Hallar el m.c.d de 344 y 1460
a) Se divide el mayor (1460) entre el menor (344); el resultado es 4 con resto 94 (primer resto)
b) Se divide el menor (344) entre el primer resto (94); el resultado es 3 con resto 62 (segundo resto)
c) Se divide el primer resto (94) entre el segundo resto (62); el resultado es 1 con resto 32 (tercer resto).
d) Se divide el segundo resto (62) entre el tercer resto (32); el resultado es 1 con resto 30 (cuarto resto).
e) Se divide el tercer resto (32) entre el cuarto resto (30); el resultado es 1 con resto 2 (quinto resto) .
f) Se divide el cuarto resto (30) entre el quinto resto (2); el resultado es 15 con resto 0.
g) El último divisor empleado es 2; por tanto el m.c.d. de 344 y 1460 es 2.

Nota. Para ahorrar tiempo y espacio estas divisiones pueden ponerse de la siguiente forma.


2- Si se trata de más de 2 números: se halla entre 2 de ellos el m.c.d.; entre éste y otro de los números se halla el m.c.d.; entre éste y otro de los números se halla el m.c.d.; y así sucesivamente: El último m.c.d. es el m.c.d. de los números dados.
Es conveniente empezar por los 2 menores.
Ejemplo:
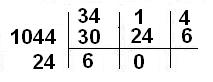
1- Hallar el m.c.d. de 300, 810 y 1044
a) Hallamos el m.c.d entre 300 y 810
Archivo:Divis sucesivas 1) .JPG
Por lo tanto el m.c.d. de 300 y 810 es 30

b) Hallar el m.c.d. de 30 y 1044

El m.c.d. (30,1044) = 6
Por lo tanto el m.c.d (300, 810, 1044) = 6

2- Hallar el m.c.d de 60, 250, 325, 500 y 600.
Como el 60 es divisor de 600 se prescinde de 600; como 250 es divisor de 500 se prescinde de éste. Entonces quedan 60, 250 y 325. Empezamos por los 2 menores

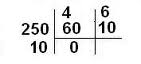
El m.c.d. de 250 y 60 es 10
Ahora hallamos el m.c.d. entre 10 y 325.

Archivo:Divs sucesivas 4) .JPG

El m.c.d de 60, 250, 325, 500 y 600 es 5.

Resumen
Debe recordarse que:
1-Si se trata de hallar el m.c.d. de dos números y uno es divisor del otro, el primero, el divisor, es el m.c.d. de los dos números dados.
2- No debe considerarse como primo un número hasta que no se haya hecho la investigación necesaria.
3- No deben suprimirse los ceros en el dividendo y el divisor al usar el método de las divisiones sucesivas.
4- Si no aparece ningún factor común entre los números dados, su m.c.d. es 1

Regla general para hallar el m.c.d. de varios números.
1- Se observa si alguno de los números dados es múltiplo de otro. En este caso se prescinde del múltiplo.
2- Se elige cuál de los métodos se va a emplear de acuerdo con lo siguiente:
• Si los número son pequeños: método de inspección
• Si lo números son grandes, pero descomposición en factores es fácil: método de descomposición en factores
• Si lo números son grandes, pero descomposición en factores es difícil: método de divisiones sucesivas.

Aplicaciones del m.c.d.

1. Simplificar una fracción hasta su irreducible.
Ejemplo: Simplifica hasta  su equivalente irreducible la siguiente fracción:

Hallamos el M.C.D. (360, 336).
Para ello factorizamos el numerador y el denominador.
360 = 2³ x 3² x 5
336 = 2⁴ x 3 x 7
Elegimos los factores primos comunes elevados al menor exponente y tenemos que:
M.C.D. (360, 336) = 2³ • 3 = 8 • 3 = 24.
Dividimos el numerador y el denominador entre 24
360 = 360 : 24 = 15
336    336 : 24    14
y obtenemos la fracción equivalente irreducible:

 2. Resolver problemas de la vida práctica.
Ejemplo: Queremos embaldosar el suelo de una cocina rectangular con baldosas cuadradas. La cocina mide 270 cm de largo por 180 cm de ancho. ¿De qué tamaño tengo que comprar las baldosas de manera que encajen enteras en estas dimensiones y sean lo más grande posible? ¿Cuántas baldosas tengo que comprar?
Solución: la longitud del lado de la baldosa ha de ser un divisor común de 270 y 180, y el más grande posible. Por lo tanto, estamos buscando el máximo común divisor de 270 y 180.
Factorizamos 270 y 180:
270 = 2 x 3³ x 5
180 = 2² x 3³ x 5
Elegimos los factores primos comunes elevados al menor exponente y tenemos que:
M.C.D. (270,180) = 2 • 3² • 5 = 2 • 9 • 5 = 90.
Por lo tanto, comprando baldosas de 90 cm de lado podremos pavimentar la cocina sin tener que romper ninguna. Ahora vamos a calcular cuántas necesitamos:
270 : 90 = 3. Tres baldosas de largo.
180 : 90 = 2. Dos baldosas de ancho.
Respuesta: Necesitamos 6 baldosas.

Ejercicios para repasar.

1. Halla el máximo común divisor de las siguientes series de números.
• 315 y 945
• 35 y 48
• 180, 252 y 594
• 924, 1.000 y 1.250

2. Hallar el número mayor que está contenido exactamente en 140, 180 y 200.
3. ¿Cuál es la mayor longitud que puede tener una cuerda con la cual es posible medir exactamente una distancia de 48 metros, otra de 64 metros y otra de 112 metros de longitud?.
4. Un ciclista puede recorrer diferentes distancias de 32, 48 o 72 Km, en un número exacto de horas. ¿Cuál es la mayor velocidad a que puede correr en esas condiciones?.
5. Si se tienen 3 depósitos de 144, 240 y 336 litros de capacidad respectivamente. Si con una manguera se puede llenar cualquiera de ellos en un número exacto de minutos. ¿Cuál es la mayor cantidad de agua que puede verter la manguera por minutos?.
6. Un ebanista quiere cortar una plancha de madera de 256 cm de largo y 96 cm de ancho, en cuadrados lo más grandes posible.¿Cuál debe ser la longitud del lado de cada cuadrado? ¿Cuántos cuadrados se obtienen de la plancha de madera?.
7. María y Jorge tienen 25 bolas blancas, 15 bolas azules y 90 bolas rojas y quieren
8. hacer el mayor número de collares iguales sin que sobre ninguna bola. ¿Cuántos collares iguales pueden hacer? ¿Qué número de bolas de cada color tendrá cada collar?
9. Un campo rectangular de 360 m de largo y 150 m de ancho, está dividido en parcelas cuadradas iguales. El área de cada una de estas parcelas cuadradas es la mayor posible. ¿Cuál es la longitud del lado de cada parcela cuadrada?
10. Juan tiene que poner un rodapié de madera a dos paredes de 12 m y 9 m de longitud. Para ello ha averiguado la longitud del mayor listón de madera que cabe en un número exacto de veces en cada pared. ¿Cuál será la longitud de este listón?

Ver también

• Múltiplos y divisores
• Mínimo Común Múltiplo.
• Divisibilidad
• Números Primos
  

Fuentes

• Sócrates Rosell Franco. Aritmética. Volumen I. Segunda Edición.
• Microsoft Encarta. Múltiplo de un número. El máximo común divisor de varios números.
• Libro de texto Secundaria Básica. 9no Grado.
• Máximo común divisor y mínimo común múltiplo.
• [1]
• [2]