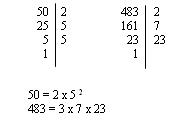Máximo común divisor
| ||||||
Máximo Común Divisor. Procedimiento matemático utilizado para resolver situaciones como la siguiente:
A un campamento de pioneros van 30 alumnos, de ellos 12 son niñas y 18 son niños, al llegar la noches estos deben acampar en cabañas. ¿De cuántas plazas, como máximo, debe ser cada cabaña para que cada una de ellas esté ocupada solo por chicos o solo por chicas?
Máximo común divisor
Máximo común divisor, de dos o más números naturales, es el mayor de sus divisores comunes.
Ejemplo: el mayor número que es divisor común de 18, 24 y 30 es 6; luego 6 es el máximo común divisor de 18, 24 y 30.
El máximo común divisor de varios números a, b, c, se designa abreviadamente así: m.c.d. (a, b, c). o también M.C.D. (a, b, c)
Para obtener el máximo común divisor de vario números naturales, existen varios métodos:
Métodos para hallar el m.c.d.
1- De acuerdo con la definición
El m.c.d. de varios números puede hallarse, de acuerdo con la definición, determinando todos los divisores, simples y compuestos, de cada uno de ellos y buscando después, entre esos divisores, cuáles son los comunes a todos los números dados. El mayor de esos divisores será el m.c.d.
Ejemplo:
a) Hallar el m.c.d. de 18, 24 y 42
Divisores de 18: 1, 2, 3, 6, 9, 18
Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24
Divisores de 42: 1, 2, 3, 6, 7, 14, 21, 42
Los divisores comunes de 18, 24 y 42 son: 1, 2, 3 y 6. El mayor es 6.
Luego el m.c.d. (18, 24, 42) = 6
Este método contribuye a aclarar el concepto de m.c.d., pero no es un método práctico, sumamente laborioso.
2- Por inspección
Se ve sucesivamente si el menor de esos números, o su mitad, o su tercera, o su cuarta, etc. (si las tiene) es divisor de los otros números dados. El primero que lo sea es el m.c.d. de todos ellos.
En cualquier caso en que un número divida a otro, el primero, el divisor, es el m.c.d. de los dos
Ejemplo:
a) Hallar el m.c.d. de 6, 18 y 24
Probamos el menor, 6 y como vemos que los otros dos son divisibles por él, el m.c.d. es 6
b) Hallar el m.c.d. de 10, 15, 45 y 90
El menor es 10, no divide a los otros. Probamos con su mitad, que es 5, y como si los divide, 5 es el m.c.d. de 10, 15, 45 y 90.
c) Hallar el m.c.d. de 6, 8 y 30
El menor es 6, no divide a los otros dos, su mitad es 3, tampoco; su tercera, 2, si los divide: por lo tanto, 2 es el m.c.d. de 6, 8 y 30.
En este método las operaciones son sencillas y se hacen mentalmente por lo que se sugiere cuando se trata de números pequeños.
3- Por descomposición en factores
Se descomponen los números dados en factores primos, se toman los factores comunes a todos ellos con el menor exponente que presenten en sus respectivas descomposiciones. El producto de esos factores será el m.c.d de los números dados.
Este método es el mejor siempre que no haya grandes dificultades para descomponer los números dados en sus factores primos.
Ejemplo:
a) Hallar el m.c.d de 180, 240 y 1400
Descomponemos los números en factores primos
Expresamos los números como productos, si algunos de los factores se repiten lo escribimos como potencia.
180 = 22 x 32 x 5
240 = 24 x 3 x 5
1400 = 23 x 52 x 7
Analizamos cada factor y observamos si están en las tres descomposiciones, de estar lo tomamos con el menor exponente, en este caso el 2 y 5 está en las tres descomposiciones, tomamos el 2 con exponente 2 (22) y el 5 con exponente 1
Luego: m.c.d (180, 240, 1400) = 22 x 5 = 4 x 5 = 20
b) Hallar el m.c.d. de 50, 100 y 483
Prescindiendo del 100 por se múltiplo de 50, resulta:
Como no hay ningún factor común el m.c.d. de 50, 100 y 483 es 1, pues sabemos que el 1 es divisor de todos los números. Esto sucede cuando los números dados son primos entre sí
4- Por divisiones sucesivas. (Hay que distinguir dos casos)
1- Si se trata de dos números: se divide el mayor por el menor, este por el primer resto, éste por el segundo, y así sucesivamente hasta llegar a una división exacta. El último divisor empleado será el m.c.d. de esos números.
Si al dividir el mayor entre el menor la división fuera exacta, el menor sería el m.c.d.
Ejemplo.
Hallar el m.c.d de 344 y 1460
a) Se divide el mayor (1460) entre el menor (344); el resultado es 4 con resto 94 (primer resto)
b) Se divide el menor (344) entre el primer resto (94); el resultado es 3 con resto 62 (segundo resto)
c) Se divide el primer resto (94) entre el segundo resto (62); el resultado es 1 con resto 32 (tercer resto).
d) Se divide el segundo resto (62) entre el tercer resto (32); el resultado es 1 con resto 30 (cuarto resto).
e) Se divide el tercer resto (32) entre el cuarto resto (30); el resultado es 1 con resto 2 (quinto resto) .
f) Se divide el cuarto resto (30) entre el quinto resto (2); el resultado es 15 con resto 0.
g) El último divisor empleado es 2; por tanto el m.c.d. de 344 y 1460 es 2.
Nota. Para ahorrar tiempo y espacio estas divisiones pueden ponerse de la siguiente forma.