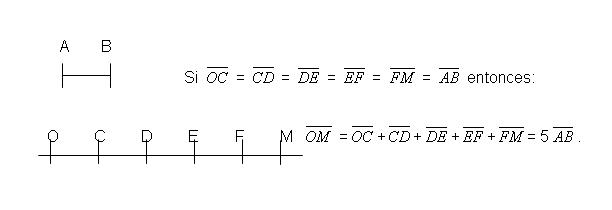Diferencia entre revisiones de «Segmento»
(→División de un segmento por un número natural) |
|||
| (No se muestran 11 ediciones intermedias de 4 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | {{Definición|Nombre=Segmento|imagen= | + | {{Definición|Nombre=Segmento|imagen=Segmento.jpg|concepto=Es la porción de [[recta]] comprendida entre dos cualesquiera de sus puntos. |
| + | }} | ||
| + | '''Segmento'''. Es la porción de [[recta]] comprendida entre dos cualesquiera de sus puntos. Los segmentos se denotan por las dos letras de sus extremos con una barra encima. Operaciones con segmentos: [[suma]], resta, [[multiplicación]] y [[división]]. | ||
== Definición == | == Definición == | ||
| − | Es la porción de recta comprendida entre dos cualesquiera de sus puntos. | + | Es la porción de [[recta]] comprendida entre dos cualesquiera de sus puntos. |
==== Representación gráfica y notación ==== | ==== Representación gráfica y notación ==== | ||
| Línea 31: | Línea 33: | ||
==== Suma de segmentos ==== | ==== Suma de segmentos ==== | ||
| − | Si AB y BC son dos segmentos consecutivos de una misma recta se llama suma de ellos el segmento AC. Se indica así: | + | Si AB y BC son dos segmentos consecutivos de una misma [[recta]] se llama [[suma]] y de ellos, el segmento AC. Se indica así: |
| − | [[Image:Suma de segmentos.JPG|center|Suma de segmentos.JPG]]Para sumar varios segmentos no consecutivos es necesario darles esta posición llevándolos sucesivamente sobre una misma recta.[[Image:Suma de segmentos no consecutivos.JPG|center|Suma de segmentos no consecutivos.JPG]] | + | [[Image:Suma de segmentos.JPG|center|Suma de segmentos.JPG]]Para sumar varios segmentos no consecutivos es necesario darles esta posición llevándolos sucesivamente sobre una misma [[recta]].[[Image:Suma de segmentos no consecutivos.JPG|center|Suma de segmentos no consecutivos.JPG]] |
=== Sustracción de segmentos === | === Sustracción de segmentos === | ||
| − | La | + | La sustracción de segmentos tiene por objeto, dados dos segmentos, llamados minuendo y sustraendo, hallar un tercero, llamado diferencia, que sumado con el sustraendo dé el minuendo.<br> |
| − | [[Image:Sustraccion de segmentos.JPG|center|Sustraccion de segmentos.JPG]] | + | [[Image:Sustraccion de segmentos.JPG|center|Sustraccion de segmentos.JPG]] |
===Multiplicación de un segmento por un número natural === | ===Multiplicación de un segmento por un número natural === | ||
| − | Multiplicar un segmento por un número natural cualquiera n, es hallar otro segmento que sea igual a n veces el segmento dado. | + | Multiplicar un segmento por un [[número natural]] cualquiera n, es hallar otro segmento que sea igual a n veces el segmento dado. |
| − | El segmento múltiplo de un segmento dado es el que se obtiene al multiplicar dicho segmento por un número natural.<br> | + | El segmento múltiplo de un segmento dado es el que se obtiene al multiplicar dicho segmento por un [[número natural]].<br> |
[[Image:Multiplicación de segmentos.JPG|center|Multiplicación de segmentos.JPG]] | [[Image:Multiplicación de segmentos.JPG|center|Multiplicación de segmentos.JPG]] | ||
| Línea 53: | Línea 55: | ||
Dividir un segmento por un [[número natural]] es hallar otro segmento que multiplicado por dicho número reproduzca el segmento dado. | Dividir un segmento por un [[número natural]] es hallar otro segmento que multiplicado por dicho número reproduzca el segmento dado. | ||
| − | [[Image:División de segmentos.JPG]]<br> Caso particular, la división de un segmento por dos que lo divide en dos segmentos iguales. | + | [[Image:División de segmentos.JPG]]<br> Caso particular, la [[división]] de un segmento por dos que lo divide en dos segmentos iguales.<br> |
| − | |||
| − | <br> | ||
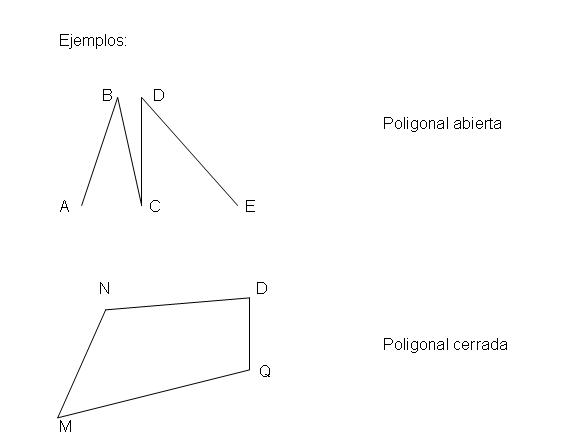
== Línea quebrada o poligonal == | == Línea quebrada o poligonal == | ||
| − | Es la figura formada por segmentos consecutivos que no están situados sobre una misma recta. Los lados de la poligonal son los segmentos que la forman. La poligonal puede ser cerrada o abierta. <br> | + | Es la figura formada por segmentos consecutivos que no están situados sobre una misma [[recta]]. Los lados de la poligonal son los segmentos que la forman. La poligonal puede ser cerrada o abierta. <br> |
[[Image:Poligonal abierta y cerrada.JPG|center|Poligonal abierta y cerrada.JPG]] | [[Image:Poligonal abierta y cerrada.JPG|center|Poligonal abierta y cerrada.JPG]] | ||
| − | La línea poligonal cerrada es aquella en la que el origen de un lado cualquiera, que se ha considerado como primero, coincide con el extremo del último. En el caso de que no coincida se dice que la poligonal es abierta. | + | La línea poligonal cerrada es aquella en la que el origen de un lado cualquiera, que se ha considerado como primero, coincide con el extremo del último. En el caso de que no coincida se dice que la poligonal es abierta. |
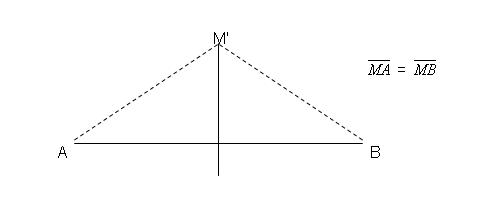
| − | == | + | ==Mediatriz de un segmento == |
| − | Es la recta perpendicular al segmento, que pasa por su punto medio.<br> | + | Es la [[recta]] perpendicular al segmento, que pasa por su punto medio.<br> |
[[Image:Mediatriz de un segmento.JPG|center|Mediatriz de un segmento.JPG]] | [[Image:Mediatriz de un segmento.JPG|center|Mediatriz de un segmento.JPG]] | ||
| Línea 75: | Línea 75: | ||
Todos los puntos de la mediatriz de un segmento equidistan de los extremos de este. | Todos los puntos de la mediatriz de un segmento equidistan de los extremos de este. | ||
| − | <br> | + | <br> |
== Fuentes == | == Fuentes == | ||
| − | + | *Miyares Arturo y Escalona Jose M. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. [[La Habana]]. [[Cuba]]. [[1974]]. | |
| − | Miyares Arturo y Escalona Jose M. Geometría, Segundo Curso. Quinta Edición. Editorial Pueblo y Educación. La Habana. Cuba. 1974. | ||
[[Category:Geometría]] | [[Category:Geometría]] | ||
última versión al 19:02 3 ago 2019
| ||||||
Segmento. Es la porción de recta comprendida entre dos cualesquiera de sus puntos. Los segmentos se denotan por las dos letras de sus extremos con una barra encima. Operaciones con segmentos: suma, resta, multiplicación y división.
Sumario
Definición
Es la porción de recta comprendida entre dos cualesquiera de sus puntos.
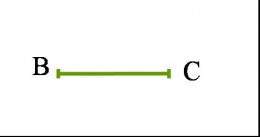
Representación gráfica y notación
Los segmentos se denotan por las dos letras de sus extremos con una barra encima.
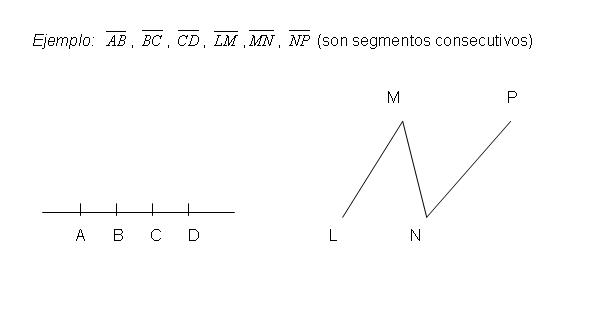
Segmentos consecutivos
Dos segmentos son consecutivos cuando tienen un extremo común.
Segmento nulo
Se llama segmento nulo a aquel cuyos extremos coinciden.
Igualdad de segmentos
Dos segmentos son iguales si superpuestos coinciden sus extremos.
Operaciones con segmentos
Suma de segmentos
Si AB y BC son dos segmentos consecutivos de una misma recta se llama suma y de ellos, el segmento AC. Se indica así:
Para sumar varios segmentos no consecutivos es necesario darles esta posición llevándolos sucesivamente sobre una misma recta.
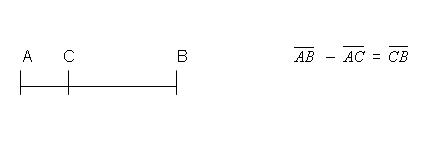
Sustracción de segmentos
La sustracción de segmentos tiene por objeto, dados dos segmentos, llamados minuendo y sustraendo, hallar un tercero, llamado diferencia, que sumado con el sustraendo dé el minuendo.
Multiplicación de un segmento por un número natural
Multiplicar un segmento por un número natural cualquiera n, es hallar otro segmento que sea igual a n veces el segmento dado.
El segmento múltiplo de un segmento dado es el que se obtiene al multiplicar dicho segmento por un número natural.
División de un segmento por un número natural
Dividir un segmento por un número natural es hallar otro segmento que multiplicado por dicho número reproduzca el segmento dado.
Caso particular, la división de un segmento por dos que lo divide en dos segmentos iguales.
Línea quebrada o poligonal
Es la figura formada por segmentos consecutivos que no están situados sobre una misma recta. Los lados de la poligonal son los segmentos que la forman. La poligonal puede ser cerrada o abierta.
La línea poligonal cerrada es aquella en la que el origen de un lado cualquiera, que se ha considerado como primero, coincide con el extremo del último. En el caso de que no coincida se dice que la poligonal es abierta.
Mediatriz de un segmento
Es la recta perpendicular al segmento, que pasa por su punto medio.
Propiedad
Todos los puntos de la mediatriz de un segmento equidistan de los extremos de este.