Teorema del binomio
→ Categoría:Teoremas de álgebra
El teorema del binomio es una ecuación que nos dice cómo se desarrolla una expresión de la forma (x+y)n para algún número natural n. Un binomio no es más que la suma de dos elementos, como (x+y). También nos permite saber para un término dado por xn-kyk cuál es el coeficiente que lo acompaña.
Este teorema es comúnmente atribuido al inventor, físico y matemático inglés sir Isaac Newton; sin embargo, se han encontrado diversos registros que indican que en el Medio Oriente ya se conocía su existencia, alrededor del año 1000.
Sumario
Historia del teorema del binomio
A lo largo de la historia, se le ha atribuido a Isaac Newton la idea del teorema del binomio, por lo que fue bautizado con su nombre, siendo popularmente conocido como el binomio de Newton. Sin embargo, el descubrimiento no viene de genialidad de este científico reconocido. Fue Al-Karjí quien aproximadamente durante el año 1000 dio inicio al desarrollo del postulado. Pero para el momento, solo se basaba en algo teórico, aunque si tenía gran validez.
Newton utilizó estas bases para desarrollar ampliamente el teorema, por lo que decidió aplicar los métodos de interpolación y extrapolación de John Wallis. Realizando ensayos en casos específicos, y usando conceptos de exponentes, logró transformar una expresión polinómica en una serie infinita.
Para 1665 amplio la teoría del postulado, alegando que n podía ser un número racional, y el siguiente año determinando que este exponente podía ser un número negativo. El resultado de aplicar este ensayo, dio a lugar una serie infinita de términos. En el último caso, decidió aplicar el triángulo de Pascal para resolver el problema con exponentes negativos.
Isaac Newton pudo detallar que cuando trabajaba con este tipo de números, la seria no tenía final. Con esto, afirmó que al utilizar un exponente negativo, se obtendrá una serie infinita. Cuando la forma (x+y) se representaba bajo el binomio (1+x), el resultado sería válido siempre que el valor de x se ubicara entre 1 y -1. En el caso de que n fuera un número racional, entonces se podrían obtener coeficientes binomiales para fracciones.
Tras realizar estas investigaciones, Newton estableció una relación entre las series infinitas y expresiones polinómicas finitas, deduciendo que en ambas se podía operar del mismo modo. Sin embargo, para el momento él no expresó ningún interés en publicar su investigación. Fue John Wallis quien mostró al público el teorema, declarando que era una contribución de Newton. Aun así, mucho tiempo antes de que se realizaran estos aportes, Euclides en el año 300 a.C. hace referencia al teorema del binomio para n=2 dentro de su ensayo Elementos. Y Stifel fue quien presentó por primera vez el término coeficiente binomial.
Declaración del teorema
Este teorema establece que cualquier potencia de un binomio x+y ser expandida en una suma de la forma:
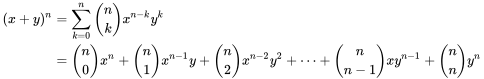
donde
![]()
es el coeficiente binomial, el cual representa el número de formas de escoger k elementos de un conjunto con n elementos.
Usando la fórmula de cálculo de dicho coeficiente, se obtiene la siguiente ecuación:
![]()
Para obtener la expansión de las potencias de una resta, basta con tomar -y en lugar de y en los términos con potencias impares:
![]()
Coeficientes binomiales
El coeficiente de xn-kyk viene dado por la fórmula
![]()
que se define en términos de la función factorial n!. De manera equivalente, esta fórmula se puede escribir
![]()
con k factores tanto en el numerador como en el denominador de la fracción. Aunque esta fórmula implica una fracción, el coeficiente binomial es en realidad un número entero.
El triángulo de Pascal
Utilizando el triángulo de Pascal, se puede emplear el teorema del binomio. Esto se define como la representación de coeficientes binomiales en forma de triángulo. Si se trabaja con tres dimensiones, se dice que se trata de una pirámide de Pascal o tetraedro de Pascal. Pasa su construcción se inicia con el número 1 en la punta del triángulo, el cual estará compuestos por nodos que se ubican en filas; la primera será enumerada 0.
Cada nodo de este árbol estará compuesto por un número del triángulo. Al sumarse dos de estos, dará a lugar al número que ocupara otro nodo en la fila de abajo. La fila 0 y la fila 1 siempre estarán compuestas solo por unos, y a partir de la dos, serán la suma de dos términos de la fila anterior.

La idea de diseñar este método fue desarrollar las potencias de binomios. Es aquí donde nace la vinculación del triángulo de Pascal con el teorema del binomio, ya que este último se expresa con la forma (x+y)n, siendo x y y cualquier variable, y n un exponente con valor de un número natural. Es a través de esta fórmula que se puede desarrollar los coeficientes de los nodos de cada fila del triángulo.
Aplicaciones
Identidades de múltiples ángulos
Para los números complejos, el teorema del binomio se puede combinar con la fórmula de De Moivre para producir fórmulas de múltiples ángulos para el seno y el coseno. Según la fórmula de De Moivre:
Usando el teorema del binomio, la expresión de la derecha se puede expandir, y luego se pueden tomar las partes real e imaginaria para obtener fórmulas para cos(nx) y sin(nx). Por ejemplo, desde:
La fórmula de De Moivre nos dice que:
que son las identidades habituales de doble ángulo. Del mismo modo, dado que
La fórmula de De Moivre rinde
En general,
y
Serie para e
El número e se define a menudo por la fórmula
Al aplicar el teorema del binomio a esta expresión se obtiene la serie infinita habitual para e. En particular:
El k-ésimo término de esta suma es
Cuando n → ∞, la expresión racional de la derecha se acerca a 1 , y por lo tanto
Esto indica que e se puede escribir como una serie:
De hecho, dado que cada término de la expansión binomial es una función creciente de n, del teorema de convergencia monótona para series se sigue que la suma de esta serie infinita es igual a e.
Probabilidad
El teorema del binomio está estrechamente relacionado con la función de masa de probabilidad de la distribución binomial negativa. La probabilidad de una colección (contable) de ensayos de Bernoulli independientes con probabilidad de éxito que no suceda es ![]()
Un límite superior útil para esta cantidad es ![]()
En álgebra abstracta
El teorema binomial es válida más generalmente para dos elementos x y y en un anillo , o incluso un semianillo, siempre que xy = yx. Por ejemplo, es válido para dos matrices n × n, siempre que esas matrices se conmuten; esto es útil para calcular las potencias de una matriz.
El teorema del binomio se puede enunciar diciendo que la secuencia polinomial {1, x, x2, x3, ...} es de tipo binomial .
En la cultura popular
- El teorema del binomio se menciona en la canción del general de división en la ópera cómica The Pirates of Penzance.
- Sherlock Holmes describe al profesor Moriarty como habiendo escrito un tratado sobre el teorema del binomio.
- El poeta portugués Fernando Pessoa, utilizando el heterónimo Álvaro de Campos, escribió que "el binomio de Newton es tan hermoso como la Venus de Milo. La verdad es que pocas personas lo notan".
- En la película de 2014 The Imitation Game, Alan Turing hace referencia al trabajo de Isaac Newton sobre el teorema del binomio durante su primer encuentro con el comandante Denniston en Bletchley Park.
Referencias
https://www.lifeder.com/teorema-binomio/
https://www.teorema.top/teorema-del-binomio/
https://www.neurochispas.com/wiki/teorema-del-binomio-ejemplos-resueltos/
https://hmong.es/wiki/Binomial_theorem

