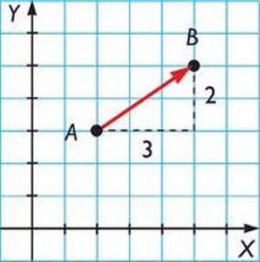
Vector
| ||||
De acuerdo con el contexto en que se use se clasifican en:
Sumario
En matemática
- Vector, en álgebra lineal, es todo segmento de recta dirigido en un espacio vectorial
- Vector (espacio euclídeo) un conjunto ordenado de números reales, o elementos de un cuerpo.
En Física
- Vector, es una herramienta geométrica utilizada para representar una magnitud física orientada.
En biología
- Vector biológico, un agente de tipo orgánico que sirve como medio de transmisión.
- Vector epidemiológico, un organismo capaz de portar y transmitir un agente infeccioso.
- Vector genético, un agente que porta un gen extraño o modificado.
- Vector viral, virus inestable modificado que permite introducir material genético exógeno en el núcleo de una célula.
- Vector de ADN es un organismo que se utiliza para transferir material genético exógeno a otra célula.
En informática y computación
- Vector de datos, un conjunto de variables del mismo tipo cuyo acceso se realiza por índices.
- Vector de interrupciones, el registro que apunta a la dirección en memoria del gestor de la interrupción.
- VectorLinux, un sistema operativo, con distribución de GNU/Linux basado en Slackware.
- Gráfico vectorial, es un dibujo realizado en un programa de diseño gráfico el cual no se distorsiona independientemente de la medida en que se imprima.
En otros contextos
- Vector, o lanzadera espacial, el vehículo de lanzamiento espacial.
- Vector energético, una forma de almacenar la energía obtenida de otra fuente durante períodos prolongados para su posterior uso.
- Vector the Crocodile, personaje de Sonic the Hedgehog SEGA.
- Vectorman, personaje de videojuego de la consola SEGA Genesis
Características de los vectores (matemáticas)
Origen
O también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector.
Módulo
Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.
Dirección
Viene dada por la orientación en el espacio de la recta que lo contiene.
Sentido
Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Clasificación de los vectores
Vectores iguales
Dos vectores son iguales cuando tienen el mismo módulo y la misma dirección.
Vector libre
Un vector libre queda caracterizado por su módulo, dirección y sentido. El vector libre es independiente del lugar en el que se encuentra.
Operaciones con vectores
Suma y resta de vectores
La suma de dos vectores libres es otro vector libre que se determina de la siguiente forma: Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el vector suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo. Por tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se suman; la otra diagonal representa la resta de dichos vectores. Propiedades Conmutativa a + b = b + a Asociativa (a + b) + c = a + (b + c) Elemento neutro o vector 0 a + 0 = 0 + a = a Elemento simétrico u opuesto a' a + a' = a' + a = 0 a' = -a
Producto de un vector por un escalar
El resultado de multiplicar un escalar k por un vector v, expresado analíticamente por kv, es otro vector con las siguientes características : 1.- Tiene la misma dirección que v. 2.- Su sentido coincide con el de v, si k es un número positivo, y es el opuesto, si k es un número negativo. 3.- El módulo es k veces la longitud que representa el módulo de v. ( Si k es 0 el resultado es el vector nulo). Analíticamente, tenemos que multiplicar el escalar por cada una de las coordenadas del vector.
Propiedades
Propiedades El producto de un vector por un escalar cumple las siguientes propiedades: 1.- Conmutativa: k · v = v · k. 2.- Distributiva: k (v + u) = (k · v ) + (k · u). 3.- Elemento Neutro: 1 · v = v. 4.- Elemento Simétrico: -1 · v = - v.
Fuentes
- http://www.tochtli.fisica.uson.mx
- http://www.vitutor.com
- Libro de Geometría Carrera Matemática