Diferencia entre revisiones de «Triángulo isósceles»
(→Propiedades) |
|||
| Línea 67: | Línea 67: | ||
|Alturas||[[Archivo:Triangulo_isosceles_alturas.png|middle]]||El [[ortocentro]] es el punto de convergencia de las alturas | |Alturas||[[Archivo:Triangulo_isosceles_alturas.png|middle]]||El [[ortocentro]] es el punto de convergencia de las alturas | ||
|- | |- | ||
| − | |Mediatrices||[[Archivo:Triangulo_isosceles_mediatrices.png|middle]]||El | + | |Mediatrices||[[Archivo:Triangulo_isosceles_mediatrices.png|middle]]||El incentro o centro de la circunferencia<br>inscrita es donde coinciden las mediatrices |
|} | |} | ||
Revisión del 19:25 30 mar 2012
| ||||||
Triángulo isósceles. En Geometría son aquellos triángulos que tienen un par de lados iguales.
La definición proviene del griego donde el término isósceles se refiere a lados equilibrados o simétricos.
Esta clase de triángulos debido a la igualdad de dicho par de lados posee un serie de propiedades que particularizan otras características geométricas y de cálculo.
Definiciones
Sea un triangulo que tenga un par de lados de longitudes iguales entre sí, se dice que es un triángulo isósceles.
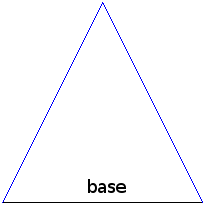
Al lado no referido como igual se le llama base del triángulo en vista a que los triángulos isósceles suelen representarse con el mismo en la parte de abajo de forma horizontal, mientras que los lados iguales apuntando hacia arriba.
Propiedades
El hecho de tener al menos un par de lados iguales permite que los triángulos isósceles tengan particularidades bien conocidas tanto en la geometría como en los cálculos de los mismos.
En primer lugar debido a la propia definición, todo triángulo equilátero es también isósceles pero evidentemente esto no es necesariamente recíproco.
Respecto a sus ángulos, el par de ángulos adyacentes a la base los denominaremos 
pues tienen igual amplitud debido a que se oponen a lados iguales dentro del mismo triángulo y el lado opuesto se denominará 
. Los lados iguales se han llamado l.
Todas las rectas fundamentales de los triángulos (altura, mediana, bisectriz, mediatriz) relativas a la base son coincidentes en el caso de los triángulos isósceles, es decir son la misma recta. Nótese que solo en el caso de los triángulos isósceles y equiláteros esta propiedad se extiende al resto de las rectas de los demás lados. Esto significa que dicha recta, llamemosla altura relativa a la base del triángulo isósceles o más simplificadamente altura divide a la mitad a la base, formando con ésta una perpendicular y también al ángulo opuesto lo divide en dos ángulos iguales a 
.
A grandes rasgos los elementos de los triángulos isósceles vienen asociados por las siguientes expresiones:
| Propiedad | Expresión |
|---|---|
| Ángulos interiores | 
|
| La mitad del ángulo opuesto a la base y el ángulo adyacente son complementarios |
|
| Relación según Pitágoras entre el lado igual la altura y la base |
4l2=4h2+b2 |
| Relaciones trigonométricas |    
|
| Teorema del seno | 
|
| Radio de la circunferencia circunscrita |
|
| Teorema del coseno | 
|
El perímetro evidentemente sería:
- PT=2l+b
Para este caso tan cómodo podemos definir el área del triángulo isósceles mediante la clásica fórmula:
En el caso de las rectas fundamentales de los triángulos isósceles, éstas se particularizan de la siguiente manera:
| Recta | Figura | Descripción |
|---|---|---|
| Medianas |  |
El centro de gravedad o baricentro se halla en:
donde (x0;y0) es el vértice opuesto a la base |
| Alturas |  |
El ortocentro es el punto de convergencia de las alturas |
| Mediatrices |  |
El incentro o centro de la circunferencia inscrita es donde coinciden las mediatrices |
La siguiente vista combinada muestra la disposición relativa de cada una de las rectas fundamentales y de sus puntos de intersección a lo largo de la altura principal:
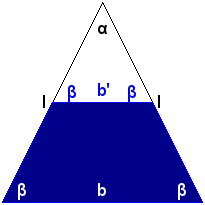
Si se traza un segmento paralelo b' a la base que seccione al triángulo en dos partes se obtiene entonces otro triángulo isósceles semejante al mayor y un trapecio isósceles cuyas bases son b y b' y los lados restantes son iguales entre sí. Este es un método común de obtención de trapecios isósceles.
Triángulos rectángulos isósceles
En el caso de los triángulos isósceles que sean rectos, la base sería la hipotenusa y los catetos los lados iguales. Obligatoriamente los ángulos de la base tendrían siempre amplitud de 45o forzando la relación entre los lados a la siguiente expresión derivada del Teorema de Pitágoras:
- b2=2l2
o desde el punto de vista trigonométrico:
El cálculo del área derivaría a la forma, ya que ahora los catetos seran alturas respectivas:
Mientras su perímetro pasa a la forma particular:
Desde el punto de vista geométrico, según el Teorema de Tales, el circuncentro ahora sería el punto medio de la hipotenusa.
Fuentes
- I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial Mir, Moscú. 1973.
- Triángulo isósceles en Wikipedia. Revisado 20 de marzo de 2012.
