Diferencia entre revisiones de «Semejanza de Triángulos»
(→Teorema fundamental de la semejanza) |
m (Texto reemplazado: «<div align="justify">» por «») |
||
| (No se muestran 25 ediciones intermedias de 5 usuarios) | |||
| Línea 1: | Línea 1: | ||
| − | |||
{{Definición | {{Definición | ||
| − | |nombre=Semejanza de Triángulos | + | |nombre= Semejanza de Triángulos |
| − | |imagen= | + | |imagen= Semejanza.jpg |
|tamaño= | |tamaño= | ||
| − | |concepto=Dos | + | |concepto= Dos [[triángulo]]s son semejantes si tienen sus [[ángulo]]s respectivamente iguales y sus lados homólogos son proporcionales. |
| − | '''Semejanza de Triángulos.''' Con el fin de llegar a comprender su significado y aplicarlo en la solución de problemas, en esta sección se analizará su concepto. | + | }} |
| − | En la práctica, para demostrar que dos | + | |
| − | == Concepto de semejanza en la vida cotidiana == | + | '''Semejanza de Triángulos.''' Con el fin de llegar a comprender su significado y aplicarlo en la solución de problemas, en esta sección se analizará su concepto. |
| + | |||
| + | En la práctica, para demostrar que dos [[triángulo]]s son semejantes, puede utilizarse el teorema fundamental de la semejanza o los criterios que aparecen a continuación. | ||
| + | == Semejanza == | ||
| + | === Concepto de semejanza en la vida cotidiana === | ||
Cuando se utiliza el término de semejanza en el lenguaje cotidiano, ¿a qué nos estamos refiriendo? Puede ser a: | Cuando se utiliza el término de semejanza en el lenguaje cotidiano, ¿a qué nos estamos refiriendo? Puede ser a: | ||
| − | |||
*Un objeto que se parece a otro. | *Un objeto que se parece a otro. | ||
*Objetos de igual tamaño. | *Objetos de igual tamaño. | ||
| Línea 15: | Línea 17: | ||
*Objetos exactamente iguales... | *Objetos exactamente iguales... | ||
| − | Es difícil poder seleccionar una opción que responda correctamente a la pregunta planteada, de acuerdo al contexto de la conversación, el significado y utilización de la palabra '''semejanza''', podría hacer referencia a objetos que se parecen en tamaño, forma o exactamente iguales, entre otros. | + | Es difícil poder seleccionar una opción que responda correctamente a la pregunta planteada, de acuerdo al contexto de la conversación, el significado y utilización de la palabra '''semejanza''', podría hacer referencia a objetos que se parecen en tamaño, forma o exactamente iguales, entre otros.<br> |
| − | |||
| − | + | '''''Resumiendo'':''' ''el uso del concepto de semejanza en el lenguaje cotidiano se refiera al "parecido", en una o más características, que existen entre dos personas u objetos.'' | |
| − | El concepto de semejanza en [[matemática]] está muy ligado al concepto de [[proporcionalidad]]. En esta ciencia se dice que dos objetos son semejantes si "guardan" una proporción entre ellos. | + | === Concepto de semejanza en matemática === |
| − | ''Resumiendo'': dos figuras son semejantes si guardan una proporción entre cada una de sus partes respectivas. | + | El concepto de semejanza en [[matemática]] está muy ligado al concepto de [[proporcionalidad]]. En esta ciencia se dice que dos objetos son semejantes si "guardan" una proporción entre ellos. |
| + | |||
| + | '''''Resumiendo''''': ''dos figuras son semejantes si guardan una proporción entre cada una de sus partes respectivas.'' | ||
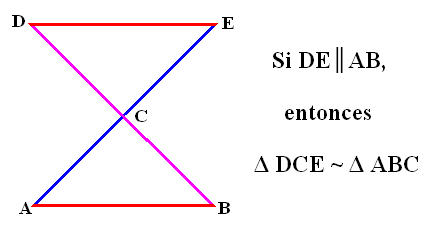
== Teorema fundamental de la semejanza == | == Teorema fundamental de la semejanza == | ||
| Línea 28: | Línea 31: | ||
[[Archivo:Semej.PNG]] | [[Archivo:Semej.PNG]] | ||
| − | + | === Criterios de semejanza === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Teorema 1:''' Si dos triángulos tienen dos ángulos respectivamente iguales, entonces son semejantes.(a.a) | |
| − | ''' | + | '''Teorema 2:''' Dos triángulos son semejantes si tienen dos lados proporcionales y el [[ángulo]] comprendido entre ellos igual.(p.a.p.) |
| − | '''Teorema:''' Si dos triángulos tienen | + | '''Teorema 3:''' Si dos triángulos tienen sus lados respectivamente proporcionales, entonces son semejantes.(p.p.p) |
| − | ( | ||
| − | ''' | + | ''Nota'': Si denominamos '''k''' la razón de semejanza entre los lados de los triángulos, entonces se cumple que: |
| − | |||
| − | ''' | + | *La razón entre sus perímetros es también '''k'''. |
| + | *La razón entre sus áreas es '''k''' 2 . | ||
| − | ''' | + | ''Nota'': la definición dada de un triángulo semejante se puede generalizar para el caso de [[polígonos]] de ''n'' lados por lo que: |
| − | ''' | + | '''Definición:''' |
| − | + | ''Dos polígonos son semejantes si tienen sus ángulos respectivamente iguales y sus lados homólogos son proporcionales. Y para ello se cumplen los mismos casos respecto a la razón entre sus lados, perímetros y áreas que las vistas para triángulos.'' | |
| − | == | + | == Enlaces externos == |
| + | * '''Semejanza y homotecia'''. Disponible en: [http://descartes.cnice.mec.es/Descartes1/4b_eso/Semejanza_y_homotecia/Homote2.htm descartes.cnice.mec.es]. | ||
| + | * Artículo: '''Geometria Interactiva'''. Disponible en: [http://www.cidse.itcr.ac.cr/ www.cidse.itcr.ac.cr]. | ||
| − | + | == Fuente == | |
*Libro de texto de Matemática 9no grado. [[Editorial Pueblo y Educación]], 1991. | *Libro de texto de Matemática 9no grado. [[Editorial Pueblo y Educación]], 1991. | ||
| − | |||
| − | [[Category: | + | [[Category:Fundamentos de la Geometría]] [[Category:Geometría]] |
última versión al 00:38 3 sep 2019
| ||||||
Semejanza de Triángulos. Con el fin de llegar a comprender su significado y aplicarlo en la solución de problemas, en esta sección se analizará su concepto.
En la práctica, para demostrar que dos triángulos son semejantes, puede utilizarse el teorema fundamental de la semejanza o los criterios que aparecen a continuación.
Sumario
Semejanza
Concepto de semejanza en la vida cotidiana
Cuando se utiliza el término de semejanza en el lenguaje cotidiano, ¿a qué nos estamos refiriendo? Puede ser a:
- Un objeto que se parece a otro.
- Objetos de igual tamaño.
- Objetos de igual forma.
- Objetos exactamente iguales...
Es difícil poder seleccionar una opción que responda correctamente a la pregunta planteada, de acuerdo al contexto de la conversación, el significado y utilización de la palabra semejanza, podría hacer referencia a objetos que se parecen en tamaño, forma o exactamente iguales, entre otros.
Resumiendo: el uso del concepto de semejanza en el lenguaje cotidiano se refiera al "parecido", en una o más características, que existen entre dos personas u objetos.
Concepto de semejanza en matemática
El concepto de semejanza en matemática está muy ligado al concepto de proporcionalidad. En esta ciencia se dice que dos objetos son semejantes si "guardan" una proporción entre ellos.
Resumiendo: dos figuras son semejantes si guardan una proporción entre cada una de sus partes respectivas.
Teorema fundamental de la semejanza
Toda recta paralela a uno de los lados de un triángulo forma, con la prolongación de los otros dos lados otro triángulo que es semejante al triángulo dado.
Criterios de semejanza
Teorema 1: Si dos triángulos tienen dos ángulos respectivamente iguales, entonces son semejantes.(a.a)
Teorema 2: Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.(p.a.p.)
Teorema 3: Si dos triángulos tienen sus lados respectivamente proporcionales, entonces son semejantes.(p.p.p)
Nota: Si denominamos k la razón de semejanza entre los lados de los triángulos, entonces se cumple que:
- La razón entre sus perímetros es también k.
- La razón entre sus áreas es k 2 .
Nota: la definición dada de un triángulo semejante se puede generalizar para el caso de polígonos de n lados por lo que:
Definición:
Dos polígonos son semejantes si tienen sus ángulos respectivamente iguales y sus lados homólogos son proporcionales. Y para ello se cumplen los mismos casos respecto a la razón entre sus lados, perímetros y áreas que las vistas para triángulos.
Enlaces externos
- Semejanza y homotecia. Disponible en: descartes.cnice.mec.es.
- Artículo: Geometria Interactiva. Disponible en: www.cidse.itcr.ac.cr.
Fuente
- Libro de texto de Matemática 9no grado. Editorial Pueblo y Educación, 1991.