¿No sabes por dónde empezar? Ayúdanos normalizando artículos.
¿Tienes experiencia? Crea alguno de estos artículos de actualidad.
Diferencia entre revisiones de «Conjunto»
(→Representación.) |
(→Pertenencia de elementos a conjuntos.) |
||
| Línea 86: | Línea 86: | ||
Para indicar que un elemento ''x'' forma parte de un conjunto ''A'' suele escribirse [[Archivo:X_en_A.gif|middle]] y se lee "'''x''' pertenece al conjunto '''A'''" o simplemente "'''x''' pertenece a '''A'''". | Para indicar que un elemento ''x'' forma parte de un conjunto ''A'' suele escribirse [[Archivo:X_en_A.gif|middle]] y se lee "'''x''' pertenece al conjunto '''A'''" o simplemente "'''x''' pertenece a '''A'''". | ||
| − | Por ejemplo: [[Archivo:12_en_pares_notacion_implicita|middle]]. | + | Por ejemplo: [[Archivo:12_en_pares_notacion_implicita.gif|middle]]. |
En caso contrario se indica [[Archivo:X_no_en_A.gif|middle]]. | En caso contrario se indica [[Archivo:X_no_en_A.gif|middle]]. | ||
Revisión del 21:20 10 jun 2011
| ||||||
Conjunto. Colección de objetos sin repetición donde el orden de éstos no importa.
Al conjunto que no contiene elementos se le llama nulo o vacío y se identifica por {} ó ![]() .
.
El conjunto de un solo elemento se denomina conjunto unitario.
El todo conjuntual tiene por nombre conjunto universo y se indica U.
Sumario
[ocultar]Representación.
Existen pautas a tener en cuanto a la hora de expresar variables que representan conjuntos y a sus elementos:
- Las variables que representan a los conjuntos se denotan con letras mayúsculas.
- Los elementos denotan minúsculas, a no ser que sean conjuntos que son miembros de otros conjuntos.
Las notaciones de conjunto como expresión escrita son básicamente dos:
- Notación extensiva o explícita.
- Notación intensiva o implícita.
En el primer caso se suele hacer la enumeración estricta de los elementos que conforman al conjunto separados por comas o punto y comas y encerrado todo entre llaves. Por ejemplo:
Como puede apreciarse en el último caso este representa al conjunto de los números pares postivos, que es infinito, por lo que se han utilizado los tres puntos suspensivos y se han escrito en un orden correcto para que el lector pueda captar qué números componen este conjunto.
Para el caso de los números reales se define un tipo especial de conjunto definido explícitamente: los rangos que en general toman las siguientes formas:
- [a; b] : Todos los números entre a y b.
- (a; b] : Todos los números entre a y b, excepto a.
- [a; b) : Todos los números entre a y b, excepto b.
- (a; b) : Todos los números entre a y b, excepto a y b.
donde a y b representan los límites del rango, a<b y los corchetes identifican que se incluye al límite correspondiente y el paréntesis que se excluye del rango al límite indicado.
En el segundo caso se escribe una ley matemática o expresión que contiene la "forma" de los elementos que van a componer al conjunto. Veánse los siguientes ejemplos:
Suele usarse la primer notación para conjuntos finitos o a partir de cuyo contenido puedan inferirse con facilidad los elementos que los componen y la segunda, para conjuntos infinitos o de una mayor complejidad en su composición porque suele ser más compacta y formal.
Representación gráfica.
También los conjuntos en dependencia de su naturaleza pueden ser representado gráficamente: líneas, superficies, cuerpos pueden ser considerados también conjuntos de puntos y tendrán su correspondiente representación.
Por ejemplo la ecuación descrita en el siguiente caso:
Tiene un conjunto solución que tiene la siguiente forma:
Como puede verse es la circunferencia de radio 1 centrada en el origen de coordenadas. Si la expresión hubiera tomado la forma x2+y2 < 1, entonces el conjunto solución sería todo el círculo dentro de la circunferencia del caso anterior pero no los puntos de la circunferencia dicha.
Por último también están los diagramas de Vern que son una representación gráfica más general de los conjuntos, muy útil para la visualización de operaciones de conjuntos. En ella, los conjuntos se representan por círculos mientras que el universo es el espacio en blanco alrededor de ellos o un recuadro que los contiene. Si los conjuntos tienen elementos en común se superpone alguna parte para indicarlo; de lo contrario, se dibujan aislados.
Operaciones de conjunto.
En los conjuntos existen tres grandes tipos de operaciones:
- Operaciones entre elementos y conjuntos.
- Pertenencia.
- Operaciones entre conjuntos.
- Subconjunto o subclase, superconjunto o superclase.
- Subconjunto propio.
- Igualdad.
- Isomorfismo o congruencia de conjuntos.
- Producto.
- Álgebra de conjuntos.
- Complemento.
- Unión.
- Intersección.
- Diferencia.
- Diferencia simétrica.
Pertenencia de elementos a conjuntos.
Para indicar que un elemento x forma parte de un conjunto A suele escribirse ![]() y se lee "x pertenece al conjunto A" o simplemente "x pertenece a A".
y se lee "x pertenece al conjunto A" o simplemente "x pertenece a A".
Subconjuntos, subconjuntos propios e igualdad de conjuntos.
Se dice que dos conjuntos A y B son iguales si ambos están conformados por los mismos elementos, independientemente del orden en que puedan aparecer y se denota A=B.
Cuando todos los elementos de un conjunto A son parte también de otro conjunto B se dice A es subconjunto de B o A es subclase de B y se indica ![]() . Si fuera el caso que todos los elementos de B estuvieran contenidos en A y no se quiere expresar como Archivo:B subconjunto A.gif, puede hacerse
. Si fuera el caso que todos los elementos de B estuvieran contenidos en A y no se quiere expresar como Archivo:B subconjunto A.gif, puede hacerse ![]() y se dice A es el superconjunto de B o A es superclase de B. Esto incluye la posibilidad de que todo conjunto es subconjunto y superclase de sí mismo, es decir
y se dice A es el superconjunto de B o A es superclase de B. Esto incluye la posibilidad de que todo conjunto es subconjunto y superclase de sí mismo, es decir ![]() y
y ![]() .
.
En cambio, los subconjuntos propios se definen como: ![]() ssi
ssi ![]() pero no A=B. Por lo que el caso Archivo:A subconjunto propio A.gif nunca se dará.
pero no A=B. Por lo que el caso Archivo:A subconjunto propio A.gif nunca se dará.
Veamos algunos ejemplos:
- Archivo:Diagramas de Vern subconjunto.png es la forma típica de representar
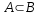 .
.  .
. .
. .
.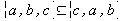 .
.- Archivo:Conjunto subconjunto ejemplo5.gif.
Una importante propiedad del conjunto vacío es que es subconjunto de cualquier conjunto, o sea ![]() .
.
Conjunto potencia.
Sea A se entiende por conjunto potencia de A al conjunto de todos los subconjuntos de A y se denota ![]() o Archivo:Rho a la A.gif.
o Archivo:Rho a la A.gif.
Ejemplos:
Isomorfismo de conjuntos.
Dos conjuntos A y B se dice que son isomorfos ssi existe una ley que asocie biunívocamente a cada elemento de A con cada elemento de B.
Ejemplos:
- El conjunto de los naturales es isomorfo con el de los números pares, pues para todo k natural existe un par de la forma 2k, o sea f(k)=2k, regla que es biyectiva.
- El conjunto de reales entre [0; 1] es isomorfo con cualquier rango [a; b], donde a y b son reales y a<b; porque para todo
 puede transformarse en
puede transformarse en 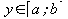 según la regla biunívoca .
según la regla biunívoca .
Producto cartesiano de conjuntos.
Sean A y B conjuntos no vacíos se define por producto cartesiano de A por B o sencillamente A por B y se denota AxB al conjunto definido por ![]() .
.
En el caso de se opere sobre el mismo conjunto se escribe como si fuera una potencia. A2=AxA, A3=AxAxA, A4=AxAxAxA.
Ejemplos:
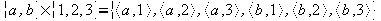 .
.- La definición cartesiana de números complejos es el producto Archivo:R x R definicion.gif.
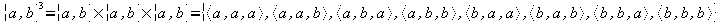
Si A es un conjunto y x es elemento de ese conjunto, se puede decir que x pertenece al conjunto A y se expresa de la siguiente manera: x Archivo:Pertenece.JPG A. De no pertenecer entonces lo escribimos de esta manera x Archivo:Nopertenece.JPG A.
Unión

Intersección
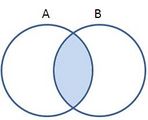
Cuando dos conjuntos no tienen elementos comunes se les llama conjuntos disjuntos y su intersección es el conjunto vacío.
Diferencia
Se define como diferencia de dos conjuntos a los elementos que están en uno que no están en el otro y se evidencia en el siguiente ejemplo:
Sean A={1,2,3,4,5} y B={3,4,5,6}
A-B = {1,2}
B-A = {6}
Complemento de un Conjunto.
Se define como complemento de un conjunto a los elementos del universo que no pertenecen a dicho conjunto. Se define de la siguiente manera:
A´= {x; xArchivo:Pertenece.JPGU y xArchivo:Pertenece.JPGA} donde U es el conjunto universo.
Cardinalidad
La cardinalidad es determinada por la cantidad de elementos que contiene un conjunto.
Por ejemplo, sea A={a,b,c,d} se puede decir que su cardinalidad es 4 y se expresa de la siguiente manera |A|=4.
Fuentes.
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción Moderna a las Matemáticas Superiores. Ediciones del Castillo, Madrid. 1967.
- Lugo, Shneidr (1969). Teoría de Conjuntos y Dominios Numéricos.
- List, G. (1977). Lógica Matemática, Teoría de Conjuntos y Dominios Numéricos.
- Brehmr, S. (1976). Analisis Matemático I.