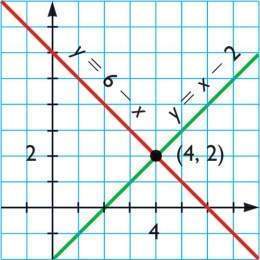
Ecuaciones lineales en una variable
Ecuaciones lineales en una variable. Son aquellas donde solo aparece una variable elevada al exponente 1. Puede usarse cualquier letra para denotar la incógnita y los coeficientes son números reales. Mediante transformaciones equivalentes se puede llevar a la forma a x + b = 0 (con a ≠ 0. El dominio de definición o dominio básico de estas ecuaciones son los valores admisibles del dominio de definición de las variables.
Sumario
- 1 Breve historia de las ecuaciones lineales
- 2 Características de las ecuaciones lineales en una variable
- 3 Reglas de la sintaxis del lenguaje algebraico
- 4 Dominio básico de una ecuación lineal
- 5 Las transformaciones equivalentes en una ecuación lineal
- 6 Procedimiento de solución de una ecuación lineal en una variable
- 7 Fuentes
Breve historia de las ecuaciones lineales
En los primeros tiempos, que comprende el período de 1700 a. de C. a 1700 d. de C., se caracterizó por la invención gradual de símbolos y la resolución de estas. Dentro de esta etapa encontramos un álgebra desarrollada por los griegos (300 a. de C.), llamada álgebra geométrica, rica en métodos geométricos para resolver ecuaciones algebraicas.
Para llegar al actual proceso de resolución de la ecuación ax + b = c han pasado más de 3 000 años. Los egipcios dejaron en sus papiros (sobre todo en el de Rhid -1.650 a. de C-) multitud de problemas matemáticos resueltos, donde se encuentran algunos que se pueden clasificar como algebraicos, pues no se refieren a ningún objeto concreto. En éstos, de una forma retórica, obtenían una solución realizando operaciones con los datos de forma análoga a como hoy se resuelven dichas ecuaciones.
Las ecuaciones más utilizadas por los egipcios eran de la forma:
x+ax=b
x + ax + bx = 0
Donde a, b y c son números conocidos y x la incógnita que ellos denominaban aha o montón.
Una ecuación lineal que aparece en el papiro de Rhid responde al problema siguiente: "Un montón y un séptimo del mismo es igual a 24".
En notación moderna, la ecuación sería: x + 1/7 x = 24
Los Babilonios (el mayor número de documentos corresponde al periodo 600 a. de C. a 300 d. de C.) casi no le prestaron atención a las ecuaciones lineales, quizás por considerarlas demasiado elementales, y trabajaron más los sistemas de ecuaciones lineales y las ecuaciones de segundo grado.
Los matemáticos griegos no tuvieron problemas con las ecuaciones lineales y, exceptuando a Diofanto (Siglo III d. de C.), no se dedicaron mucho al álgebra, pues su preocupación era mayor por la Geometría.
Sobre la vida de Diofanto aparece en los siglos V o siglo VI un epigrama algebraico que constituye una ecuación lineal:
- Transeúnte, ésta es la tumba de Diofanto: es él quien con esta sorprendente distribución te dice el número de años que vivió. Su juventud ocupó su sexta parte, después durante la doceava parte su mejilla se cubrió con el primer vello. Pasó aún una séptima parte de su vida antes de tomar esposa y, cinco años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle, llorándole durante cuatro años. De todo esto, deduce su edad.
Características de las ecuaciones lineales en una variable
El lenguaje algebraico, como todo lenguaje consta de un sistema de signos, unas relaciones entre ellos para formar frases, una sintaxis y una semántica.
El conjunto de signos con sentido forman una frase.
La semántica estudia la correspondencia entre significantes y significados y permite distinguir de entre las frases correctamente formadas, aquellas que tienen significado. La sintaxis algebraica estudia las reglas a que han de someterse los símbolos para formar frases algebraicamente correctas.
Hoy día el Álgebra no es “dar significado” a los símbolos, sino otro nivel más allá de eso; tiene que ver con aquellos modos de pensamiento que son esencialmente algebraicos –por ejemplo- manejar lo todavía desconocido, invertir y deshacer operaciones, ver lo general en lo particular. Ser consciente de esos procesos y controlarlos, es lo que significa pensar algebraicamente.
Reglas de la sintaxis del lenguaje algebraico
- Los signos de las operaciones no pueden ir seguidos.
- La letra que designa la incógnita funcionará como un número.
- El signo igual (=) no puede ir al lado del signo de las operaciones.
- Los signos de las operaciones y el de la igualdad no pueden empezar ni acabar frase.
Dominio básico de una ecuación lineal
Un dominio numérico, se denomina dominio básico de una ecuación lineal, si y solo si este dominio numérico es el dominio de individuos para la variable contenida en la ecuación.
Al sustituir la variable de la ecuación lineal por símbolos que denotan elementos apropiados de su dominio básico, esta ecuación se transforma en una proposición. El conjunto de elementos que la transforma en una proposición verdadera es su conjunto solución.
Una ecuación de la forma a x + b = 0 (con a ≠ 0; a, b Є R) en un dominio básico de solución dado que contenga más de un elemento, tiene:
- Ninguna solución, cuando al sustituir la variable por cada uno de los elementos del dominio básico no se obtiene proposición verdadera alguna.
- Exactamente una solución, cuando al sustituir la variable por los elementos del dominio básico, se obtiene una proposición verdadera en un único caso.
Las transformaciones equivalentes en una ecuación lineal
Toda transformación de una ecuación lineal que no conduce a ningún cambio, en el dominio básico de solución dado, se denomina transformación equivalente de la ecuación.
Dentro de las principales transformaciones equivalentes de las ecuaciones lineales están:
- Las que se realizan en cada miembro de la ecuación.
- Supresión de paréntesis.
- Colocación de paréntesis.
- Simplificación y ampliación de fracciones numéricas.
- Aplicación de la ley conmutativa de la adición y de la multiplicación.
- Agrupación de términos (adición, multiplicación, etcétera).
- Supresión de paréntesis.
- Las que se realizan en ambos miembros de la ecuación al mismo tiempo. Estas son transformaciones que se pueden fundamentar mediante la ley de monotonía.
- Adición o sustracción a ambos miembros de la ecuación, de un término T definido para todos los valores de de la variable, que se pueden sustituir en la ecuación.
- Multiplicación o división de ambos miembros de la ecuación por un término, que para todas las sustituciones permisibles de la variable toma valores diferentes de cero.
- Adición o sustracción a ambos miembros de la ecuación, de un término T definido para todos los valores de de la variable, que se pueden sustituir en la ecuación.

Procedimiento de solución de una ecuación lineal en una variable
- Por reflexiones lógicas: consiste en determinar cuál es el valor de la variable que satisface la ecuación planteada mediante operaciones que se realizan mentalmente.
- Por un procedimiento algorítmico: consiste en realizar una serie de pasos para obtener la solución, que se pueden seguir como un modelo.
- Formar la ecuación, si parte de una situación problémica.
- Agrupar términos semejantes en cada miembro de la ecuación.
- Reducir términos semejantes.
- Despejar la variable.
- Calcular el valor de la variable.
- Comprobar que el valor obtenido satisface la ecuación o la situación problémica.
- Escribir el conjunto solución o dar la respuesta, si partió de una situación problémica.
Fuentes
- Ministerio de Educación (1980): Teoría elemental de los números, Ecuaciones y Combinatoria. La Habana: Editorial de libros para la Educación.
- Muñoz Baños, F. et al (2001): Matemática de Séptimo grado. La Habana: Editorial Pueblo y Educación.
- Muñoz Baños, F. et al (2005): Matemática de Octavo grado. La Habana: Editorial Pueblo y Educación.
- Quintana Valdés, A. et al (2005): Matemática 8. Grado, Cuaderno Complementario. La Habana: Editorial Pueblo y Educación.
- Ribnikov, K. (1987): Historia de las Matemáticas. Moscú: Editorial Mir.
- Rizo Cabrera, C. et al (1996): Matemática 6. La Habana: Editorial Pueblo y Educación.