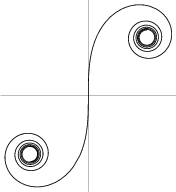
Espiral de Cornu
| ||||||
Espiral de Cornu o Clotoide. Se nombra en honor de Marie Alfred Cornu. Es una curva tangente al eje de las abcisas en el origen y cuyo radio de curvatura disminuye de manera inversamente proporcional a la distancia recorrida sobre ella.
Ecuación
- La expresión matemática usual es:
ρs=C siendo
ρ el radio de curvatura
s el desarrollo o arco
C la constante de la espiral
- Las ecuaciones paramétricas de la espiral de Cornu vienen dadas por S(t) y C(t):
C‘(t)2+S‘(t)2=sin2(t2)+cos2(t2)=1 En esta parametrización el vector tangente tiene longitud unidad y t es la longitud de arco medida a partir de (0,0) (e incluyendo signo), de lo que se deduce que la curva tiene longitud infinita.
Historia
Esta curva se descubrió en la era de la geometría diferencial, donde se hizo precisa la noción de curvatura como la proporción en que la curva cambia de dirección. A la espiral de Cornu se le asignó este nombre por el científico francés Marie Alfred Cornu(1841-1902), quien la estudio en relación con la difracción de la luz. A partir de los trabajos de Cornu esta curva se uso con amplitud en el cálculo de la difracción de la luz. También conocida como clotoide o espiral de Euler, este último nombre debido a que fue Euler quien empezó a estudiar la curva (1744) en una investigación sobre la elasticidad de un resorte Esta curva puede ser parametrizada por las integrales de Augustin Jean Fresnel, las cuales son bien conocidas en la teoría de difracción.
Aplicaciones
En el punto origen de la curva, el radio es infinito y se usa en la construcción de carriles de aceleración y deceleración en las autovías, autopistas, vías ferroviarias y montañas rusas.