Diferencia entre revisiones de «Geometría analítica galileana»
(Página creada con '{{Definición|Nombre=Geometría Analítica Galilena|imagen=Fig 2 Geo.JPG|}} '''Geometria Analitica Galileana'''. Rama de la Geometría Analítica que describe el conjunto d...') |
|||
| Línea 18: | Línea 18: | ||
[[Imagen:fig 1 Parabolaaa.JPG|thumb|left|250px|Parábola]]. | [[Imagen:fig 1 Parabolaaa.JPG|thumb|left|250px|Parábola]]. | ||
| − | La parábola pertenece a una familia de curvas llamadas cónicas, formada por ella, la elipse y hipérbola. Estas otras curvas no se definen de la misma manera que la parábola. | + | La parábola pertenece a una familia de [[curvas]] llamadas [[cónicas]], formada por ella, la [[elipse]] y [[hipérbola]]. Estas otras curvas no se definen de la misma manera que la parábola. |
==Análisis== | ==Análisis== | ||
| − | Como un mismo ente se puede definir desde dos puntos de vista diferentes (como ocurre con el concepto de límite que puede ser definido según el criterio de Heine que lo hace por medio de sucesiones, y además según el criterio de Cauchy que utiliza la idea de infinitesimales) podemos hacer un análisis para intentar definir la hipérbola y la elipse desde el mismo punto de vista que hicimos con la parábola. En principio queremos definir movimiento de | + | Como un mismo ente se puede definir desde dos puntos de vista diferentes (como ocurre con el concepto de límite que puede ser definido según el criterio de [[Heine]] que lo hace por medio de [[sucesiones]], y además según el criterio de [[Cauchy]] que utiliza la idea de [[infinitesimales]]) podemos hacer un análisis para intentar definir la hipérbola y la elipse desde el mismo punto de vista que hicimos con la parábola. En principio queremos definir movimiento de unpunto que se tiene lugar de la misma manera respecto a otros dos puntos. En [[Geometría Analítica]] se muestra que la recta puede considerarse como el punto que se mueve de la misma manerarespecto a dos puntos fijos o sea al moverse mantiene la misma distancia respecto a ambos. Veamos la ecuación para representar esta situación usando la definición de distancia mediante el [[Teorema de Pitágoras]]. |
[[Imagen: 1 x-0 +y.JPG|thumb|left|250px|es lo mismo que escribir]].[[Imagen: 2 x-0 + y-0.JPG|thumb|right|250px|si eliminamos los radicales]]. | [[Imagen: 1 x-0 +y.JPG|thumb|left|250px|es lo mismo que escribir]].[[Imagen: 2 x-0 + y-0.JPG|thumb|right|250px|si eliminamos los radicales]]. | ||
| Línea 36: | Línea 36: | ||
| − | Esta ecuación es la representación analítica o algebraica del enunciado en lenguaje común | + | Esta ecuación es la representación [[analítica]] o [[algebraica]] del enunciado en lenguaje común de que en un sistema de [[coordenadas cartesianas]] un punto de coordenadas (x; y) se mueve por el plano respecto a dos puntos fijos de ese plano de coordenadas (0; 0) y (h; k) de manera tal que las distancias del punto (x; y) a estos son iguales.Si en esta ecuación desarrollamos los cuadrados y simplificamos, la ecuación obtenida puede escribirse de la forma. |
2- ) | 2- ) | ||
la cual es sin lugar a dudas la ecuación de una recta pues está escrita de la forma | la cual es sin lugar a dudas la ecuación de una recta pues está escrita de la forma | ||
2.1-) que es la ecuación segmentaria de la recta. | 2.1-) que es la ecuación segmentaria de la recta. | ||
| − | Los movimientos que se describen usando el Teorema de Pitágoras los llamaremos euclidianos. | + | Los movimientos que se describen usando el Teorema de Pitágoras los llamaremos [[euclidianos]]. |
| − | Pero los movimientos de los que estamos hablando deben transcurrir por cónicas, o sea que en general su ecuación debe ser de la forma | + | Pero los movimientos de los que estamos hablando deben transcurrir por [[cónicas]], o sea que en general su ecuación debe ser de la forma |
| − | 3- ) la cual comparada con la 2.1 es notorio que solo se diferencian en el grado que tienen las variables y los parámetros. Y como la forma 2.1 se obtuvo de 1.1 que es de grado dos , las ecuaciones de la forma 3-) deben poderse obtener de una similar pero de grado tres ,o sea por medio de una ecuación de la forma | + | 3- ) la cual comparada con la 2.1 es notorio que solo se diferencian en el grado que tienen las [[variables]] y los [[parámetros]]. Y como la forma 2.1 se obtuvo de 1.1 que es de grado dos , las ecuaciones de la forma 3-) deben poderse obtener de una similar pero de grado tres ,o sea por medio de una ecuación de la forma |
3.1-) | 3.1-) | ||
| − | Y debe ser la que describe el lugar geométrico de un punto que se mueve describiendo una cónica siguiendo el Principio de Galileo, o sea el punto de coordenadas (x; y) se mueve de la misma forma respecto a los puntos (0; 0) y (h; k) pudiéndose considerar uno de estos fijo y el otro en movimiento uniformemente. | + | Y debe ser la que describe el lugar geométrico de un punto que se mueve describiendo una cónica siguiendo el [[Principio de Galileo]], o sea el punto de coordenadas (x; y) se mueve de la misma forma respecto a los puntos (0; 0) y (h; k) pudiéndose considerar uno de estos fijo y el otro en movimiento uniformemente. |
Si desarrollamos, tendremos: | Si desarrollamos, tendremos: | ||
| Línea 53: | Línea 53: | ||
Que tiene como expresión final | Que tiene como expresión final | ||
| − | La cual es la ecuación de una elipse imaginaria. Aquí podemos hacer | + | La cual es la ecuación de una [[elipse imaginaria]]. Aquí podemos hacer |
. Si dividimos la primera ecuación entre la segunda tendremos la igualdad | . Si dividimos la primera ecuación entre la segunda tendremos la igualdad | ||
| − | de la que se deduce por el producto k*1/h que k y 1/h son las pendientes de los diámetros conjugados de una hipérbola según el teorema del geómetra Apolonio de Pérgamo. Esta relación, elipse imaginaria e hipérbola es la que existe entre las geometrías de Euclides y de Minkowsky. | + | de la que se deduce por el producto k*1/h que k y 1/h son las pendientes de los diámetros conjugados de una hipérbola según el teorema del geómetra [[Apolonio de Pérgamo]]. Esta relación, elipse imaginaria e hipérbola es la que existe entre las geometrías de [[Euclides]] y de [[Minkowsky]]. |
| − | + | Ahora nos queda por buscar un esquema geométrico que muestre que la elipse puede ser descritadel mismo modo que la parábola. Esto lo haremos usando una simplificación del método usado comúnmente para demostrar que la elipse, la hipérbola y la parábola son [[secciones cónicas]], el cual está basado en el uso de esferas tangentes a un cono. Veamos la fig.2. | |
[[Imagen:fig2 Geoelipse.JPG|thumb|left|250px|Elipse]]. | [[Imagen:fig2 Geoelipse.JPG|thumb|left|250px|Elipse]]. | ||
==Argumentación== | ==Argumentación== | ||
| − | El plano α corta al cono y su interseccion o sean los puntos comunes forman una elipse. Como el plano α es tangente a la esfera en el punto F, el haz de rectas del plano que pasa por este punto es tangente a la esfera | + | El plano α corta al cono y su interseccion o sean los puntos comunes forman una elipse. Como el plano α es tangente a la esfera en el punto F, el haz de rectas del plano que pasa por este punto es tangente a la esfera. Como el cono es tangente a la esfera , las generatrices de este son tangentes a ella , y por el conocido teorema referido a las tangentea de una circunferencia estan en un mismo plano y se cortan, tienen la misma longitud se cortan por lo que los segmentos son iguales en longitud. El observador situado en el punto F ve el mismo conjunto de puntos que aquel que se mueve unformemente por la circunferencia interseccion entre la esfera y el cono. Variando la inclinacion del plano se obtienen las graficas de la parabola y la hiperbola. |
==Conclusion== | ==Conclusion== | ||
Revisión del 21:21 7 may 2012
| ||||
Geometria Analitica Galileana. Rama de la Geometría Analítica que describe el conjunto de conocimientos congruentes con el principio de Galileo y que es el punto de partida para la descripción de los fenómenos naturales.
Sumario
Fundamentación
Uno de los propósitos básicos de las matemáticas es suministrar un lenguaje simbólico y elegante mediante el cual se puedan describir los hechos del mundo físico. Esto quiere decir que por medio de ese lenguaje se puede expresar el problema físico dado en forma de relaciones cuantitativas. Por ejemplo las expresiones trigonométricas es el lenguaje que permite describir los hechos periódicos, y de ahí el uso para exponer y resolver estos hechos; el análisis vectorial es el formulismo o lenguaje adecuado para exponer y resolver la teoría del campo electromagnético, ya que este expresa las características esenciales de ese estado. Esto no puede hacerse en muchos casos si no se tiene en cuenta que la Geometría es el vinculo que une el mundo físico con el lenguaje analítico-algebraico. Además para cada hecho no se puede construir un lenguaje y buenas estaría todas las ciencias en general si para cada hecho necesitara un lenguaje. El poder de un simbolismo radica en que mediante él se puedan describir multitud de hechos físicos, aquellos que abarcan, con una sola cadena de ecuaciones hechos del mundo físico exteriormente no semejantes pero que en esencia transcurren geométricamente del mismo modo, y pueden ser considerados desde el mismo punto de vista.
Principio de Galileo Galilei
Las leyes de la naturaleza son descritas por ecuaciones de la misma forma tanto por los observadores cuyos móviles están en reposo, como por aquellos cuyos móviles están animados de movimiento uniforme. Es necesario disponer de un esquema geométrico que permita representar este hecho , y que permita construir una ecuación que describa el movimiento o movimientos que cumplen estas condiciones: que sea el mismo tanto para un observador cuyo móvil esta en reposo como para aquel cuyo móvil esta en movimiento.
La Parábola
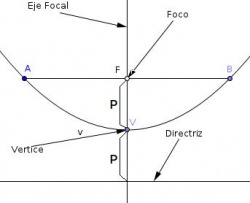
Por definición la parábola es el conjunto de los puntos de un plano que se mueven por este plano de manera tal que sus distancias a un punto F fijo de este llamado foco son las mismas que las que tienen los puntos de esta a una recta contenida en este plano y es llamada directriz. Ver la figura 1
.La parábola pertenece a una familia de curvas llamadas cónicas, formada por ella, la elipse y hipérbola. Estas otras curvas no se definen de la misma manera que la parábola.
Análisis
Como un mismo ente se puede definir desde dos puntos de vista diferentes (como ocurre con el concepto de límite que puede ser definido según el criterio de Heine que lo hace por medio de sucesiones, y además según el criterio de Cauchy que utiliza la idea de infinitesimales) podemos hacer un análisis para intentar definir la hipérbola y la elipse desde el mismo punto de vista que hicimos con la parábola. En principio queremos definir movimiento de unpunto que se tiene lugar de la misma manera respecto a otros dos puntos. En Geometría Analítica se muestra que la recta puede considerarse como el punto que se mueve de la misma manerarespecto a dos puntos fijos o sea al moverse mantiene la misma distancia respecto a ambos. Veamos la ecuación para representar esta situación usando la definición de distancia mediante el Teorema de Pitágoras.
..
Esta ecuación es la representación analítica o algebraica del enunciado en lenguaje común de que en un sistema de coordenadas cartesianas un punto de coordenadas (x; y) se mueve por el plano respecto a dos puntos fijos de ese plano de coordenadas (0; 0) y (h; k) de manera tal que las distancias del punto (x; y) a estos son iguales.Si en esta ecuación desarrollamos los cuadrados y simplificamos, la ecuación obtenida puede escribirse de la forma.
2- )
la cual es sin lugar a dudas la ecuación de una recta pues está escrita de la forma
2.1-) que es la ecuación segmentaria de la recta.
Los movimientos que se describen usando el Teorema de Pitágoras los llamaremos euclidianos.
Pero los movimientos de los que estamos hablando deben transcurrir por cónicas, o sea que en general su ecuación debe ser de la forma 3- ) la cual comparada con la 2.1 es notorio que solo se diferencian en el grado que tienen las variables y los parámetros. Y como la forma 2.1 se obtuvo de 1.1 que es de grado dos , las ecuaciones de la forma 3-) deben poderse obtener de una similar pero de grado tres ,o sea por medio de una ecuación de la forma 3.1-)
Y debe ser la que describe el lugar geométrico de un punto que se mueve describiendo una cónica siguiendo el Principio de Galileo, o sea el punto de coordenadas (x; y) se mueve de la misma forma respecto a los puntos (0; 0) y (h; k) pudiéndose considerar uno de estos fijo y el otro en movimiento uniformemente.
Si desarrollamos, tendremos:
y simplificando , y completando cuadrados perfectos se obtiene :
que es lo mismo que
Que tiene como expresión final
La cual es la ecuación de una elipse imaginaria. Aquí podemos hacer . Si dividimos la primera ecuación entre la segunda tendremos la igualdad de la que se deduce por el producto k*1/h que k y 1/h son las pendientes de los diámetros conjugados de una hipérbola según el teorema del geómetra Apolonio de Pérgamo. Esta relación, elipse imaginaria e hipérbola es la que existe entre las geometrías de Euclides y de Minkowsky.
Ahora nos queda por buscar un esquema geométrico que muestre que la elipse puede ser descritadel mismo modo que la parábola. Esto lo haremos usando una simplificación del método usado comúnmente para demostrar que la elipse, la hipérbola y la parábola son secciones cónicas, el cual está basado en el uso de esferas tangentes a un cono. Veamos la fig.2.
.Argumentación
El plano α corta al cono y su interseccion o sean los puntos comunes forman una elipse. Como el plano α es tangente a la esfera en el punto F, el haz de rectas del plano que pasa por este punto es tangente a la esfera. Como el cono es tangente a la esfera , las generatrices de este son tangentes a ella , y por el conocido teorema referido a las tangentea de una circunferencia estan en un mismo plano y se cortan, tienen la misma longitud se cortan por lo que los segmentos son iguales en longitud. El observador situado en el punto F ve el mismo conjunto de puntos que aquel que se mueve unformemente por la circunferencia interseccion entre la esfera y el cono. Variando la inclinacion del plano se obtienen las graficas de la parabola y la hiperbola.
Conclusion
De la ecuacion 3.1) que puede ser escrita de la forma
3.2)
Se deduce que la ecuación 3.3) l= describe el movimiento uniforme en el espacio de un punto de coordenadas (x; y) respecto al punto de coordenadas (a; b) con independientemente del estado de reposo, o de movimiento uniforme del móvil del observador situado en el.
Fuentes
- Artículo:www.monografías.com /Principio Único de las Teorías Físicas. Disponible en "www. monografías.com". Consultado el 10 de noviembre del 2011.
- Artículo: [Teórica]. Disponible en "www.ecured.cu". Consultado el 20 de Abril del 2012.