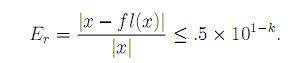Matemática numérica
| ||||||
Matemática Numérica. Es una rama de la Matemática (del lat. mathematĭca, y éste del gr. μαθηματικά, derivado de μάθημα, conocimiento) en la cual el objetivo no es el estudio de un ente matemático en particular; la Matemática Numérica tiene como propósito el desarrollo de métodos para la solución de los más diversos problemas matemáticos mediante una cantidad finita de operaciones numéricas. Es decir, lo que le da unidad a esta rama de la Matemática, no es el tipo de problema que se ha de resolver sino el método que se aplicará: operaciones numéricas en cantidad finita.
Está claro que, por regla general, los problemas matemáticos no pueden ser resueltos exactamente de esta manera. Por eso, la Matemática Numérica no se plantea llegar a resultados exactos; ni siq uiera a resultados tan exactos como sea posible. El propósito aquí será obtener resultados tan exactos como sea necesario. Los métodos de solución que emplea la Matemática Numérica reciben el nombre gen érico de métodos numéricos y, en contraposición, a los otros métodos matemáticos se les llamará métodos analíticos. El prescindir de la exactitud absoluta, permite a la Matemática Numérica elaborar métodos mucho más generales que los métodos analíticos exactos. Como se trata de métodos numéricos (solo se requieren operaciones aritméticas, no operaciones algebraicas de tipo simbólico) estos métodos pueden ser fácilmente implementados en una computadora digital. Por todas estas razones, la Matemática Numérica posee en la actualidad una gran importancia.
Sumario
Historia
Aunque, como ciencia estructurada y rigurosa, la Matemática Numérica es relativamente joven (siglos XIX y XX), desde tiempos muy remotos se emplearon métodos numéricos aproximados. En el papiro de Rhind (el documento matemático más antiguo que se conserva) que data de unos 2000 años a. n. e., fruto del desarrollo de la antigua civilización egipcia, aparecen, entre más de 80 problemas resueltos, métodos aproximados para calcular el volumen de un montón de frutos y el área de una circunferencia, tomándola como la de un cuadrado cuyo lado fuera 8/9 del diámetro de la circunferencia. En Babilonia (siglos XX al III, a. n. e.) ya se conocían métodos aproximados para calcular raíces cuadradas. De la antigua Grecia, son famosos los trabajos de Arquímedes (siglo III a. n. e.) en la Cuadratura del círculo que le permitió, aproximando una circunferencia mediante polígonos inscritos y circunscritos, llegar a una aproximación.
Sobre los conocimientos matemáticos de la cultura egipcia los primeros registros que se tienen son el Papiro de Moscú y de Rhind, escritos aproximadamente en 1850 A. de C. y 1650 A. de C., respectivamente. Ambos documentos incluyen ejemplos de cálculos que implican el manejo de ecuaciones lineales con una y dos incógnitas. En cuanto a geometría, determinaron con éxito el área y el volumen de diversas figuras geométricas: entre ellas, el volumen de una pirámide truncada.
Es con los griegos que aparece por primera vez, en el siglo V A.de C., la matemática como una ciencia formal que utiliza el método deductivo como herramienta fundamental para probar que un resultado es verdadero. Los teoremas que se atribuyen a Tales de Mileto y a Pitágoras son algunos de los primeros ejemplos en el que se aplica esta metodología y el libro de los Elementos de Euclides es la muestra más acabada de ello. La matemática griega se ocupó de estudiar problemas de geometría, aritmética, teoría de números y álgebra.
Arquímedes (287-212) es posiblemente el más brillante matemático aplicado de la antigüedad; a él se deben diversos ejemplos de métodos muy ingeniosos para aproximar la solución de problemas de la hidrodinámica y estática. Escribió más de diez obras; entre ellas el estudio de las cónicas, de la esfera y el cilindro, sobre la espiral y sobre el cálculo de volúmenes de revolución de elipses, parábolas e hipérbolas que giran alrededor de un eje de simetría y el cálculo del área de una parábola. Desde finales del siglo XVII comienza a perfilarse la teoría de las series infinitas, ligadas a matemáticos como el suizo Euler, el alemán Leibniz y los ingleses Newton y Taylor sin las cuales hubiera sido imposible justificar o deducir muchos de los métodos numéricos que se estudiaran más adelante.
El método de Arquímedes fue posteriormente aplicado por otros matemáticos y ya en la primera mitad del siglo XV el árabe Kashi había obtenido para π una aproximación de 17 cifras decimales utilizando polígonos de hasta 805 306 368 lados. Un notable ejemplo de cálculos numéricos son las tablas de logaritmos publicadas en 1614 por el holandés Neper en que aparecen, con 8 cifras exactas, los logaritmos de las funciones trigonométricas para ángulos desde 0 hasta 90 grados con paso de un minuto. Gracias al gigantesco trabajo numérico del propio Neper y de otros como el suizo Bürgi, el escocés Briggs y el holandés Vlacq ya en 1628 existían tablas de logaritmos decimales de los números desde 1 a 100 000 calculadas con 10 cifras decimales exactas.
Desde la aparición de los primeros asentamientos humanos se usaron piedras, cordeles, varillas como instrumentos de medición y cálculo; posteriormente, la aparición del ábaco facilitó enormemente el cálculo aritmético. La introducción de la notación decimal y del cero en el siglo XII por los árabes uniformó la notación y el cálculo numérico entre los diversos pueblos. Pero no fue sino hasta inicios del siglo XVII, con el invento de las tablas de logaritmos, que el cálculo numérico experimentó un avance fundamental para el desarrollo de la ciencia en el siglo Siglo_XVII y XVIII. La tabla de logaritmos fue creada por John Napier (1550-1617), quien fue de los primeros en estudiar la notación y el manejo de distintas bases numéricas como la binaria o la exponencial. Sus estudios sobre la relación entre las progresiones geométricas y aritméticas lo llevaron a definir el logaritmo base 1/e que publicó en 1615.
Al morir Napier, su amigo Henry Briggs (1561-1630), el primer profesor saviliano de geometría de Oxford, retoma y simplifica su trabajo con el fin de generalizarlo a cualquier base, en particular la base decimal, que publica en 1617 con una precisión de catorce cifras. Con la tabla de logaritmos, las multiplicaciones de varias cifras se convierten en simples sumas y el elevar un número a un exponente se reduce a una simple multiplicación. Esto permitió abordar problemas de astronomía, de balística y de índole práctico que parecían incalculables. Poco después, hizo su aparición en 1624 la regla de cálculo que permaneció como instrumento personal de cálculo por excelencia hasta la aparición de las primeras calculadoras de bolsillo en 1970.
Con estos antecedentes los precursores del cálculo: Descartes, Fermat, Pascal, Wallis, Barrow y Gregory, entre otros, desarrollaron la geometría analítica, diversos métodos para determinar la ecuación de la tangente a una curva dada; el cálculo de máximos y mínimos y el cálculo de cuadraturas, entre otros temas. Estos resultados prepararon el terreno para que, a fines del siglo XVII, Leibnitz y Newton los sistematizaran, relacionaran y unificaran en una metodología poderosísima: el cálculo diferencial e integral.
A principios del siglo XVIII se produce otro gran paso con la aparición del Cálculo de Diferencias Finitas (fundado por los ingleses Taylor y Stirling), el cual constituye la base teórica para fundamentar varios métodos numéricos.
Figuras como Isaac Newton (1642-1727) hicieron aportes fundamentales para definir con precisión el concepto de velocidad instantánea, la fuerza de atracción entre los cuerpos, la fuerza gravitacional y la descomposición de la luz, entre otras muchas cosas. Desde el punto de vista numérico, Newton inventó varios algoritmos que se siguen utilizando hasta nuestros días, como el método para encontrar los ceros de una función o la aproximación de derivadas por medio de diferencias divididas o la construcción de polinomios de interpolación.
En esa misma época se introdujo el uso de series de potencias que permitió aproximar localmente con la precisión deseada a un gran conjunto de funciones y abrió la posibilidad de atacar problemas de mayor complejidad que aparecen en el estudio de fenómenos físicos como las vibraciones de una cuerda, la difusión de calor o el comportamiento de los fluidos. Por ejemplo, James Gregory (1638-1675) en 1671 determinó la serie de potencias para la función Arctang(x) lo que permitió aproximar, tanto como se deseara, el valor de π
(π/4) = 1 – (1/3) + (1/5) – (1/7) +…
Siguiendo el ejemplo de Newton, varios matemáticos de primer orden contribuyeron a la solución de problemas numéricos: Leonard Euler (1707-1783) utilizó la serie de Taylor para crear el método que lleva su nombre y que aproxima la solución de problemas con condiciones iniciales en ecuaciones diferenciales ordinarias; Joseph Louis Lagrange (1736-1813) dio una forma de construir polinomios de interpolación. Karl Friedrich Gauss (1777-1855) contribuyó de manera notable con el método de mínimos cuadrados y sus fórmulas de cuadratura que abren la puerta a la utilización de familias de polinomios ortogonales para la aproximación de integrales; sus aportes al estudio de la solución de sistemas de ecuaciones lineales siguen siendo fundamentales en la enseñanza del álgebra lineal. También se le atribuye la invención de la transformada rápida de Fourier, algoritmo que pasó desapercibido hasta su redescubrimiento por Cooley y Tukey en 1963.
Durante la segunda mitad del siglo XIX, la matemática entró en una etapa de rigorismo necesario para cimentar con firmeza su amplio cuerpo de conocimientos Weierstrass y Cauchy entre otros, son los responsables del concepto riguroso de límite que es fundamental en el análisis. Esto explica que la obtención de cálculos numéricos pasara a segundo término aunque el desarrollo del análisis funcional está estrechamente ligado a la aproximación de funciones en espacios normados. Por último, hay que mencionar que, a principios del siglo XX, Richardson aplicó por primera vez el método de diferencias finitas para el análisis de esfuerzos en distintos materiales y que, en 1928 apareció el famoso artículo de Courant, Friedrichs y Lewy sobre el análisis de estabilidad de estos métodos. Para saber más sobre la historia del análisis numérico, consultar.
El surgimiento y consolidación del Análisis Funcional desde finales del siglo XIX hasta principios del XX, permitió a la Matemática Numérica dar un salto cualitativo al lograrse esclarecer los conceptos básicos de la aproximación funcional. Con el surgimiento de las computadoras digitales a mediados del siglo XX y su continuo desarrollo, la Matemática Numérica ha recibido un fuerte estímulo, ya que la computadora digital ha hecho posible la aplicación práctica de muchos métodos numéricos, que con el trabajo en forma manual, solo tendrían un valor teórico. Por otra parte, las computadoras digitales han traído la necesidad de desarrollar nuevos métodos numéricos para dar respuesta a nuevos problemas que antes no era posible siquiera imaginar.
Fuentes de error
El hecho de que la Matemática Numérica ponga su atención en métodos aproximados, no significa que los errores carezcan de importancia; todo lo contrario: un método aproximado solo tiene valor si permite, de alguna forma, tener una estimación de la magnitud del error que se comete con su aplicación. Por esta razón, es necesario dedicar un tiempo a estudiar los diversos tipos de errores que se pueden presentar en la solución de un problema real. En la figura 1 se muestra esquemáticamente los pasos que suelen seguirse para llegar a la solución de un problema real y los errores que pueden introducirse en los diferentes pasos. Pudiera pensarse que el camino a seguir es tratar de eliminar todas las fuentes posibles de error, pero no es así: algunos tipos de error son inevitables y, como se verá, algunos resultan aconsejables.
Modelación y sus errores
El primer paso en la solución de un problema consiste en pasar de una situación problémica del mundo real a un
modelo matemático. Este modelo matemático consiste generalmente en un conjunto de objetos matemáticos relacionados entre sí, tales como ecuaciones diferenciales, integrales, ecuaciones e inecuaciones algebraicas, tablas, esquemas, etc. que intentan reflejar (no copiar) los aspectos esenciales del mundo real que constituyen la situación problémica del mundo natural. Este paso suele llamarse modelación matemática del problema.
Nótese que el modelo no puede, ni debe, reflejar exactamente el mundo real sino sólo los aspectos de aquel que resultan importantes en el problema que se desea resolver, de acuerdo con el uso que se dará a los resultados obtenidos. Realmente, la modelación matemática tiene mucho de arte; si el modelo copia demasiados detalles de la realidad, es probable que el modelo matemático sea tan complicado que no ayude a comprender lo esencial del problema, e incluso, que no pueda ser resuelto posteriormente; si se ignoran aspectos importantes del mundo real entonces puede ocurrir que el modelo sea una aproximación demasiado grosera de la realidad y que se pueda llegar a conclusiones absurdas a partir del modelo.
El arte consiste en decidir adecuadamente qué aspectos del mundo real deben estar reflejados en el modelo y cuáles no, de manera que los errores de modelación sean aceptables para los objetivos que se persigue. Por ejemplo, para la mayoría de los problemas de mecánica se suele suponer que la aceleración producida por la fuerza de la gravedad es 9,8 m/seg2, independientemente del lugar de la tierra en que ocurra el fenómeno; en realidad esta acele ración varía desde 9,780 en el ecuador hasta 9,832 en las regiones polares; esta suposición no causa grandes e rrores en problemas comunes pero en el lanzamiento de cohetes propulsores de satélites artificiales, hay que tener en cuenta la aceleración gravitacional propia de cada lugar de La Tierra por donde vuele el cohete pro pulsor, pues de otra forma se introducen errores (de modelación) intolerables.
A los efectos de la Matemática Numérica, los errores de modelación suelen clasificarse (junto con los de medición) como errores inherentes, en el sentido de que no pueden ser eliminados o disminuidos por el tratamiento matemático del problema, ya que están presentes desde la misma formulación del problema.
Errores de truncamiento
La segunda etapa en la solución de un problema es establecer los métodos o algoritmos que se usarán para la solución del modelo matemático planteado. A veces estos métodos son exactos pero, casi siempre esto no es posible o no es práctico. La mayoría de los métodos exactos solamente se aplican a situaciones muy simples y específicas que raras veces se dan en los problemas reales. Por ejemplo, las ecuaciones algebraicas de grado mayor que 4 solamente se pueden resolver por métodos exactos cuando poseen soluciones enteras o racionales (el método de Rufini) lo cual siempre sucede en los problemas escolares pero casi nunca en la realidad; las ecuaciones no algebraicas (es decir, las trigonométricas, logarítmicas, exponenciales, etc.) solo admiten soluciones por métodos exactos en casos muy triviales; los métodos de integración exactos, basados en hallar una primitiva del integrando, pueden aplicarse a un reducido número de integrales y en problemas tan simples como calcular la longitud de una elipse, fracasan rotundamente.
Por todas estas razones, en una gran cantidad de ocasiones hay que recurrir a métodos no exactos en la solución del modelo matemático obtenido. El error que se introduce en el proceso debido a la no exactitud del método de solución empleado se suele llamar error de truncamiento. Esta palabra se utiliza debido a que muchas veces la no exactitud del método utilizado proviene de utilizar en alguna parte de un proceso, solo una cantidad finita de términos de una serie infinita (es decir, de truncar una serie). Sin embargo, no es esta la única causa de que un método no sea exacto; a veces el error se produce por sustituir una derivada por un cociente finito de incrementos o una integral por una suma finita de muchos sumandos pequeños o por detener un proceso infinito convergente. A lo largo de este libro serán tratados muchos métodos aproximados y en cada caso se hará el estudio necesario del error de truncamiento cometido, que a veces se llama simplemente, error del método.
Errores en el proceso de cálculo
Una vez que está definido el algoritmo de solución del modelo matemático, se procede a la solución. En la actualidad, la solución se ejecuta, en su mayor parte, mediante calculadora electrónica o mediante una computadora digital con un programa adecuado. En esta etapa del proceso se pueden introducir tres tipos de errores:
Errores de observación
Estos son los errores contenidos en los datos debido a la imperfección de los instrumentos de medición o los métodos de observación utilizados o a la poca información acerca del problema que se está resolviendo. A veces, los objetivos que se persiguen no justifican utilizar datos de mayor calidad, los cuales pueden ser muy costosos. Por ejemplo, medir una temperatura con un error menor que 0,01 grados centígrados requiere instrumentos sumamente costosos que pocos laboratorios en el mundo poseen en la actualidad y, posiblemente, el resultado que se desea obtener no se afecte grandemente por este pequeño error de medición. Como ya se mencionó, los errores de medición (junto con los de modelación) forman parte de los llamados errores inherentes, dado su carácter externo al procesamiento matemático del modelo.
Equivocaciones
En el trabajo manual estos son esos frecuentes errores que se introducen, por ejemplo, cuando se dice que “tres por dos es cinco” o cuando se oprime una tecla equivocada en la calculadora. Con el uso de las computadoras las equivocaciones no suelen ocurrir en el momento en que se ejecuta el programa, pero sí pueden estar presentes en el programa elaborado y sus consecuencias pueden a veces pasar inadvertidas durante años. Cuando el trabajo numérico se realizaba a mano, los algoritmos de cálculo se ejecutaban mediante tablas y en ellas siempre aparecían “columnas de comprobación”, destinadas a realizar operaciones redundantes solamente con el objetivo de detectar las equivocaciones. Con el uso de las computadoras digitales, el proceso de detección y corrección de equivocaciones (que suele llamarse debuging en el argot de los programadores) es una etapa muy importante de la puesta a punto de un programa, pero se escapa a los objetivos de un curso de Matemática Numérica.
Errores de redondeo
Estos errores se producen cuando se sustituye un número decimal por otro con menos cifras. Más adelante se profundizará en este tipo de errores pero por el momento puede adelantarse que ellos están constantemente presentes tanto si se trabaja a mano, como si se usa una calculadora o una computadora sofisticada. Son debidos a la naturaleza del sistema de numeración que se utiliza, el cual se basa en cifras y no permite representar todos los números reales mediante una cantidad finita de dígitos. Por ejemplo, cuando se utiliza 0,333333 en lugar de 1/3 ó 3,1416 en lugar de π , se comenten errores de redondeo.
A diferencia de las equivocaciones ante las cuales todo lo que se puede hacer es tratar de evitarlas, con los errores de redondeo hay que aprender a convivir; ellos son inevitables y todo lo que se necesita es, por una parte, mantenerlos lo suficientemente pequeños de modo que no afecten significativamente los resultados que se desea obtener y, por otra parte, no intentar hacerlos exageradamente pequeños (por ejemplo, utilizando una cantidad muy grande de cifras decimales) porque ello se traduce en algoritmos innecesariamente lentos.
Ejemplos
Ejemplo#1
Desde un cierto punto del espacio se lanza un pequeño objeto al suelo (por ejemplo, una piedrecilla) y se desea saber que distancia recorrerá en su trayectoria desde la mano hasta el piso.
Solución: Primero es necesario modelar matemáticamente el problema. Como es un problema mecánico, hay que recurrir a las leyes de la Mecánica para elaborar un modelo adecuado. En el proceso de modelación habrá que realizar algunas aproximaciones que introducirán errores de modelación.
Se tomarán las siguientes hipótesis:
- La partícula lanzada se tratará como si fuera un punto.
- Se considerará que la partícula solamente es atraída por la Tierra y no por la Luna o por otros cuerpos celestes.
- Se tomará el valor de 9,8 m/seg2 como la aceleración de la gravedad.
- Se ignorará el efecto de la fuerza de empuje del aire sobre la partícula.
- No se tomará en cuenta la fricción entre el aire y la partícula.
- Se supondrá que el aire está en reposo, es decir, que no hay viento.
- Se aproximará la superficie del suelo como un plano perfectamente horizontal.
Todas estas hipótesis son idealizaciones que permitirán llegar a un modelo matemático suficientemente sencillo, a costa de introducir errores de modelación. Se supone que el error de modelación introducido es razonablemente pequeño a los efectos del resultado que se desea obtener. Uno de los primeros pasos en la modelación matemática de un problema, es la definición de un sistema de referencia adecuado. Se tomará el instante en que la piedra es lanzada (en que abandona la mano) como el instante inicial (t = 0). En cuanto al sistema de referencia espacial, se tomará un plano coordenado con su eje x colocado en el suelo y el eje y vertical pasando por el punto en que la partícula abandona la mano. El eje x se toma en una dirección tal, que la trayectoria de la partícula se efectúa en plano xy. En la figura 2 se muestra el sistema de referencia, la partícula en su posición inicial (en blanco) y en un instante t posterior (en negro) y, en línea de puntos, la trayectoria que supuestamente seguirá.
Para obtener el modelo matemático se hará uso de la conocida Segunda Ley de Newton de la Mecánica: “La suma de las fuerzas que actúan sobre una partícula es igual al producto de su masa por su aceleración”. Esta ley establece una igualdad vectorial, que puede expresarse como dos igualdades escalares, tomando las componentes respectivas de la fuerza resultante y de la aceleración:
Fx = max (1)
Fy = may (2)
En un instante t = 0 cualquiera, según la hipótesis iniciales, la única fuerza que actúa sobre la partícula es la debida a la atracción gravitacional, que es una fuerza vertical dirigida hacia abajo y de magnitud mg. De aquí resulta Fx = 0 y Fy = – mg. Sustituyendo en las ecuaciones (1) y (2):
max = 0 (3)
may = – mg (4)
De las ecuaciones (3) y (4) se obtienen de forma inmediata:
ax = 0 (5)
ay = – g (6)
Como la aceleración es la segunda derivada del desplazamiento respecto al tiempo, las ecuaciones (5) y (6) se traducen en:
(d²x) / (dt²) = 0 (7)
(d²y) / (dt²) = -g (8) donde t = 0.
Para completar el modelo matemático hay que añadir a las ecuaciones (7) y (8) las condiciones iniciales del problema, algunas de las cuales son consecuencia del sistema de referencia definido:
x (0) = 0 (9)
y (0) = h (10)
vx (0) = v0 x (11)
v y (0) = v0 y (12)
donde h, v0x y v0y son datos del problema que habrá que obtener por medición.
Las ecuaciones (7) a (12) constituyen el modelo matemático del problema. Operando con este modelo matemático se pueden predecir muchas cosas: la trayectoria de la partícula, el lugar en que esta choca con el suelo, la máxima altura que alcanza en su recorrido, etcétera. Como el problema que se desea investigar es la distancia que recorre la piedra en su trayectoria, será necesario trabajar con el modelo para obtener:
Aplicaciones en la computación
Hay muchas formas de representar los números, desde la antigüedad se conocen las ventajas de utilizar potencias de 10 lo que da un sistema posicional decimal en el que es importante la posición que ocupa un dígito. Usar las potencias de diez es natural porque los humanos tienen diez dedos en la mano, pero hay otros sistemas que utilizan las potencias de otros números. Los babilónicos tenían un sistema sexagesimal y quedan vestigios de ello en nuestra forma de medir el tiempo. Para las computadoras lo más natural es usar potencias de dos, ya que almacenan los caracteres en bytes que a su vez se componen de 8 bits. Cada bit puede tomar dos valores, uno si está prendido y cero si está apagado. Un byte permite representar 256 caracteres distintos.
Una palabra de computadora se compone de 4 bytes y una palabra doble de 8 bytes consecutivos. Al usar potencias de dos se dice que se trabaja en base binaria en lugar de la base decimal. Algunas computadoras modernas trabajan en base octal, base 8, o hexadecimal que es en base 16.
La manera más fácil de representar un número real en una computadora es en notación de punto flotante. A continuación, por simplicidad, se presenta esta notación en base decimal aunque las computadoras usan otras bases. La notación es la siguiente:
X = +- d1d2d3……..dkdk+1…….. X 10^n
donde n es un número entero, dk es un número entero entre 0 y 9, y d1 es distinto de cero. La sucesión de dígitos dk se le conoce como la mantisa y al entero n como el exponente.
Como la representación de un número real puede tener mantisa infinita y n puede tomar cualquier valor en los enteros, es imposible que un instrumento de cálculo pueda representar cualquier número en forma exacta; cada instrumento de cálculo tiene una cota superior e inferior para n y solo puede almacenar un número finito de dígitos k de la mantisa. Si se almacena un real con exponente mayor a n; la computadora marca un error que se conoce como overflow o desbordamiento superior. Si el real tiene como exponente un entero menor a la cota inferior, la máquina genera un error de underflow o desbordamiento inferior. Cuando la mantisa tiene un número de dígitos mayor a k entonces la computadora redondea el número y almacena solo k dígitos.
El procedimiento de redondear consiste en lo siguiente: primero se observa el valor del dígito dk+1; si este es menor o igual a 4 se almacenan únicamente los primeros k dígitos; si dk+1 es mayor o igual a 5 se suma un uno al k-ésimo dígito y se almacenan los k dígitos del número resultante.
Para representar un número en punto flotante se puede usar una palabra simple o doble, la diferencia estriba en el número de dígitos k de la mantisa que almacenan. Si se usan palabras simples para representar a los reales se dice que se calcula en simple precisión o en doble precisión en caso de utilizar palabras dobles.
¿De qué tamaño es el error que se comete al representar cualquier número real en una computadora? Para estimarlo denótese por fl(x) la representación en punto flotante de un número real x en una computadora con una mantisa de k dígitos. Se usará el error relativo Er para estimar el error y se puede probar que
Véase también
- Funciones matemáticas
- Matemática
- Matemática Discreta
- Análisis Matemático
- Elementos de lógica matemática
Bibliografía
- Benjamin, Peirce (1882). Linear Associative Algebra. Van Nostrand. Digitalizado por University of California Libraries. Págs. 97-229.
- Einstein, Albert (1923). «Geometry and experience», en Sidelights on relativity. P. Dutton., Co.
- Peterson, Ivars. (2001). Mathematical Tourist, New and Updated Snapshots of Modern Mathematics. Owl Books. ISBN 0-8050-7159-8.
- Jourdain, Philip E. B., «The Nature of Mathematics», en The World of Mathematics. Courier Dover Publications. ISBN 0-486-41153-8.
- Waltershausen, Wolfgang Sartorius von (1856, repr. 1965). Gauss zum Gedächtniss. Sändig Reprint Verlag H. R. Wohlwend. ISBN 3-253-01702-8.
- Popper, Karl R. (1995). «On knowledge», en In Search of a Better World: Lectures and Essays from Thirty Years. Routledge. ISBN 0-415-13548-6.
- Ziman, J.M., F.R.S. (1968). Public Knowledge:An essay concerning the social dimension of science. Cambridge University Press.
- Riehm, Carl (August 2002). «The Early History of the Fields Medal», en Notices of the AMS. AMS 49 (7). Págs. 778–782.