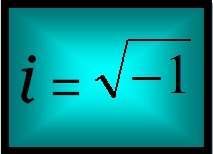Números imaginarios
| ||||||
Números imaginarios. Son números complejos cuya parte real es igual a cero. Un número imaginario puede describirse como el producto de un número real por la unidad imaginaria i, donde la letra i denota la raíz cuadrada de -1. Al número imaginario i se le denomina también constante imaginaria.
Sumario
Surgimiento de los números imaginarios
Su nombre fue acuñado por René Descartes en el Siglo XVII y lo propuso con intenciones despectivas aunque es un concepto válido, suponiendo un plano con ejes cartesianos en el que los números reales se encuentran sobre el eje horizontal y los imaginarios sobre el eje vertical complejo.
Para agregarle mitología además de llamarlo número imaginario, se le hizo pertenecer al conjunto de los números complejos. Si no conocemos el valor real de i, por lo menos sí sabemos que i elevada a la potencia i es un número irracional conocido como: I = ii, por ejemplo: I = ii = 0,20787958140365… y este es un número imaginario que es muy real.
Historia
En el año 1777, Leonhard Euler le dio el nombre de i, por imaginario, de manera despectiva (i = √¯-1) dando a entender que no tenían una existencia real.
Gottfried Wilhelm Leibniz, en el siglo XVII, expresó "El Espíritu divino se manifestó sublimemente en esta maravilla del análisis, en este portento del mundo de las ideas, este anfibio entre el ser y el no ser, que llamamos raíz imaginaria de la unidad negativa".
En 1572, Rafael Bombelli ya había realizado cálculos utilizando números imaginarios pero sin utilizar aún la letra i, y en 1811, Jean-Robert Argand crea la representación gráfica del Plano complejo también conocida como plano de Argand.
Notación de un número imaginario
Un número imaginario se denota por bi, donde: b es un número real e i es la unidad imaginaria: √¯-1 = a i. Cada número imaginario puede ser escrito también como i·r donde r es un número real e i es la unidad imaginaria.
Los valores de las potencias de la unidad imaginaria se repiten de cuatro en cuatro. Los números imaginarios permiten calcular raíces con índice par y radicando negativo.
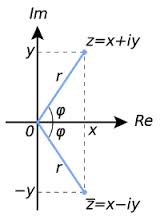
Interpretación geométrica
Geométricamente, los números imaginarios se encuentran en el eje vertical del plano complejo, presentándolos como perpendiculares al eje real. Una manera de ver los números imaginarios es considerando una recta numérica típica, que aumenta positivamente hacia la derecha y aumenta negativamente hacia la izquierda.
Podemos dibujar un eje de coordenadas vertical pasando por el 0 del eje horizontal, de modo que represente números imaginarios aumentando positivamente hacia arriba y negativamente hacia abajo. Este eje vertical es llamado el "eje imaginario" y es denotado como i, R, ∏ o simplemente ₰.
En esta representación, una multiplicación por –1 corresponde a una rotación de 180° sobre el origen. Una multiplicación por i corresponde a una rotación de 90° en la dirección "positiva" (en el sentido antihorario), y la ecuación i ² = -1 puede interpretarse diciendo que si aplicamos dos rotaciones de 90° sobre el origen, el resultado final es equivalente a una simple rotación de 180°. Una rotación de 90° en la dirección "negativa" (sentido horario) satisface también esta interpretación. Esto refleja el hecho que -i es también una solución de la ecuación x² = -1.
En general, multiplicar por un número complejo es lo mismo que sufrir una rotación alrededor del origen por el argumento del número complejo, seguido de un redimensionamiento a escala por su magnitud.
Propiedades
- Partiendo de que la raíz cuadrada de cualquier número real negativo, da por resultado un número imaginario (por ejemplo: √¯-36 = √¯(-36) (-1) = √¯36 √¯-1 = 6 i ).
- Un número imaginario es un número cuyo cuadrado es negativo ( i² = -1 ) .
- Estos números extienden el conjunto de los números reales al conjunto de los números complejos.
- Los números imaginarios, al igual que los números reales, no pueden ser ordenados de acuerdo a su valor.
- Para los números imaginarios no se cumple: 1 > 0 y -1 < 0.
- Los números imaginarios formalmente no pertenece al conjunto de los números reales ni al conjunto de los números racionales.
- El número imaginario es tan real como cualquier otro natural, entero o fraccionario, ya que se ocupa igualmente para describir la realidad, y es tan racional y entendible como cualquier número irracional.
- Estos tienen una infinita cantidad de decimales.
- Al multiplicar un número complejo por la unidad imaginaria rota un ángulo e 90º, pero mantiene su valor absoluto.
- Uno de los valores de ii es un número real. [1]
Uso de los números imaginarios
- El número imaginario no solo es imprescindible en Física y Matemática, sino que ha `permitido la ampliación y desarrollo de nuevos conceptos.
- Tiene especial utilidad en electromagnetismo, ondas radiactivas, trayectorias espaciales, hidrodinámica e indispensables para múltiples problemas matemáticos.
- La unidad imaginaria puede ser usada para extender formalmente la raíz cuadrada de números negativos y las raíces cuartas, sextas y pares de números negativos, confirmando el teorema fundamental del álgebra. Esto es toda ecuación algebraica de grado n, con coeficientes complejos, tiene por lo menos una raíz en el campo de los números complejos.
- Igualmente la raíz cuadrada de un número imaginario es un número complejo, y la raíz de un número complejo en general es otro número complejo.
- En física cuántica la unidad imaginaria permite simplificar la descripción matemática de los estados cuánticos variables en el tiempo.
- En teoría de circuitos y corriente alterna la unidad imaginaria se usa para representar ciertas magnitudes como fasores, lo cual permite un tratamiento algebraico más ágil de dichas magnitudes.
- En campos de la ingeniería eléctrica y afines, la unidad imaginaria es a menudo escrita como j para evitar la confusión con la intensidad de la corriente eléctrica, tradicionalmente denotada por i.
Fuente
- Artículo Número imaginario. Disponible en: es.wikipedia.org. Consultada el 1 de julio de 2014.
- M. Perdigao do Carmo- A. C. Morgado- E. Wagner. Trigonometría y números complejos. IMCA, LIMa, 1999. ISBN 9972-05-0
Referenciasy notas
- ↑ üsese i = eipi/2
Véase también
- Número real
- Ecuaciones algebraicas.
Sitios consultados
- Vitutor, disponible en: www.vitutor.com. Consultada el 2 de julio de 2014.
- Iboenweb, disponible en: www.iboenweb.com. Consultada el 2 de julio de 2014.
- Ditutor, disponible en: www.ditutor.com. Consultada el 2 de julio de 2014.