Diferencia entre revisiones de «Números irracionales»
(→Representación en la recta real) |
(→Representación en la recta real) |
||
| Línea 37: | Línea 37: | ||
Los números irracionales π y e por citar algunos, se representan usando su expansión decimal ubicando en la [[recta]] aproximadamente su lugar (respetando el orden).<br> | Los números irracionales π y e por citar algunos, se representan usando su expansión decimal ubicando en la [[recta]] aproximadamente su lugar (respetando el orden).<br> | ||
En el caso de algunos números irracionales como ± √2, ± √3, ± √5±,… pueden representarse exactamente en la [[recta]] mediante el uso de una [[regla]] y [[compás]]<br> | En el caso de algunos números irracionales como ± √2, ± √3, ± √5±,… pueden representarse exactamente en la [[recta]] mediante el uso de una [[regla]] y [[compás]]<br> | ||
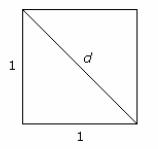
| − | Por ejemplo, para representar ± √2 consideramos un [[triángulo rectángulo | + | Por ejemplo, para representar ± √2 consideramos un [[triángulo rectángulo]] equilátero de catetos 1, con uno de sus vértices en el origen de la [[recta]] (ver figura 1). Luego con un [[compás]] trazamos una [[circunferencia]] de radio la [[hipotenusa]] de dicho [[triángulo]] (que es √2). La intersección de esta [[circunferencia]] con la [[recta]] real es el número √2 a la derecha, y -√2 a la izquierda (ver figura 1). De manera análoga se puede representar ± √5. En este caso, se toma un [[triángulo rectángulo]] de catetos 1 y 2, tal como se muestra en la figura. <br> |
Figura 1 | Figura 1 | ||
Revisión del 15:28 4 sep 2012
| ||||||
Números irracionales . Son los elementos de la recta real que no pueden expresarse mediante el cociente de dos enteros y se caracterizan por poseer infinitas cifras decimales no periódicas. De este modo, puede definirse al número irracional como un decimal infinito no periódico.
Sumario
Número irracional
Los números irracionales surgen por la imposibilidad de resolver en Q ciertos problemas. Por ejemplo, si se quiere calcular la longitud de la diagonal de un cuadrado de lado 1, esto no es posible hacerlo en el conjunto de los números racionales, ya que por el Teorema de Pitágoras, llamando d a la longitud buscada, se ha de cumplir que:
d2 = 12 + 12 = √2, de donde, d = √2 que no es un números racionales puesto que no se puede expresar como una fracción, en otras palabras, la expresión decimal √2 tiene infinitas cifras decimales.
El conjunto de los números irracionales se representa por I y está formado por todos los números decimales cuya parte decimal tienen infinitas cifras periódicas, es decir, por todos los números que no se pueden representar por el cociente de dos números enteros. Es inmediato que no existe ningún número que sea racional e irracional, es decir, Q C I =Ø
Números irracionales famosos
Clasificación
Números Algebraicos, son aquellos que provienen de la solución de alguna ecuación algebraica y se representan por un número finito de radicales libres o anidados. Por ejemplo:
En general, todas las raíces no exactas de cualquier orden son irracionales algebraicos.
Números Trascendentales, no pueden representarse mediante un número finito de raíces libres o anidadas; provienen de las llamadas funciones trascendentes: trigonométricas, logarítmicas y exponenciales. El número Pi (π) y Euler (e) son irracionales trascendentes, puesto que no pueden expresarse mediante radicales. Los irracionales trascendentes también surgen al escribir números decimales no periódicos al azar o con un patrón que no lleva periodo definido. Por ejemplo:
0,1234567891011121314151617181920212223...
1,01001000100001000001000000100000001...
Representación en la recta real
Representar un número con infinitas cifras decimales no periódicas es imposible y por lo tanto nos tendríamos que conformar con una aproximación. De todas maneras, hay métodos geométricos que permiten representar algunos números irracionales en la recta numérica.
Los números irracionales π y e por citar algunos, se representan usando su expansión decimal ubicando en la recta aproximadamente su lugar (respetando el orden).
En el caso de algunos números irracionales como ± √2, ± √3, ± √5±,… pueden representarse exactamente en la recta mediante el uso de una regla y compás
Por ejemplo, para representar ± √2 consideramos un triángulo rectángulo equilátero de catetos 1, con uno de sus vértices en el origen de la recta (ver figura 1). Luego con un compás trazamos una circunferencia de radio la hipotenusa de dicho triángulo (que es √2). La intersección de esta circunferencia con la recta real es el número √2 a la derecha, y -√2 a la izquierda (ver figura 1). De manera análoga se puede representar ± √5. En este caso, se toma un triángulo rectángulo de catetos 1 y 2, tal como se muestra en la figura.
Figura 1
Operaciones con números irracionales
Las operaciones de suma, resta, multiplicación y división no son operaciones bien definidas en los números irracionales, dados dos números irracionales no siempre la suma, resta, multiplicación o división de dichos números resulta un número irracional En cuanto a las operaciones con números irracionales es necesario tener en cuenta lo siguiente:
Sin embargo y a pesar de su extraño comportamiento tenemos dos afirmaciones que siempre son válidas:
- Si es racional y b es irracional entonces la suma a + b siempre es irracional.
- Si a ≠ 0 es racional y b es irracional entonces el producto a ·b siempre es irracional.
En virtud de estas afirmaciones podemos decir que:
2+ √3 es irracional.
2 · √5 es irracional