Diferencia entre revisiones de «Razones y proporciones»
(→Razón entre números) |
(→Proporciones) |
||
| Línea 22: | Línea 22: | ||
Hay que saber distinguir entre los conceptos de razón y de fracción. Este último alude a la relación también multiplicativa entre la parte y el todo respectivo. En el ejemplo anterior, 2/5 representa la fracción ya simplificada correspondiente al número de hombres (18) con respecto al total de personas presentes (18 + 27 = 45). En el concepto de razón no está presente esta relación de carácter parte-todo. | Hay que saber distinguir entre los conceptos de razón y de fracción. Este último alude a la relación también multiplicativa entre la parte y el todo respectivo. En el ejemplo anterior, 2/5 representa la fracción ya simplificada correspondiente al número de hombres (18) con respecto al total de personas presentes (18 + 27 = 45). En el concepto de razón no está presente esta relación de carácter parte-todo. | ||
| + | <br /> | ||
==Proporciones== | ==Proporciones== | ||
La igualdad entre dos razones es una proporción. | La igualdad entre dos razones es una proporción. | ||
| − | + | ||
| − | |||
| − | |||
Se lee: | Se lee: | ||
*'''a''' es a '''b''' como '''c''' es a '''d'''. | *'''a''' es a '''b''' como '''c''' es a '''d'''. | ||
| Línea 37: | Línea 36: | ||
[[Image:Teorema propor.JPG]] | [[Image:Teorema propor.JPG]] | ||
| + | |||
| + | Un ejemplo de proporción es 2/3 = 4/6, cuya lectura es “2 es a 3 como 4 es a 6”. De nuevo hay que recordar la distinción entre razones y fracciones, para no ver en la expresión anterior “la equivalencia de dos fracciones” (que será la lectura correcta cuando se hable de fracciones, pero no ahora...). | ||
| + | |||
| + | Vamos con la nomenclatura relativa a las proporciones. El uso de la notación a : b : :c : d nos ayuda a identificar a los números a y d como los extremos de la proporción y a los números b y c como los medios de la proporción. Por ejemplo, en 2/3 = 4/6, 2 y 6 son los extremos de la proporción, y 3 y 4, los medios. | ||
| + | |||
| + | Una proporción cuyos extremos y medios son diferentes se denomina discreta; por ejemplo, la anterior. Y continua, si los medios(o los extremos) son iguales entre sí; su forma sería: a/b = b/c ó a/b = c/a. Por ejemplo, 2/6 =6/18. En una proporción discreta, cualquier término se denomina cuarta proporcional de los otros tres. Así, en el ejemplo 2/3 = 4/6 decimos que 3 es cuarta proporcional de 2,4 y 6, ó que 4 lo es de 2, 3 y 6. En una proporción continua, el término repetido se denomina media proporcional de los otros dos, y estos dos últimos, tercia proporcional del otro término. Así, en el ejemplo 2/6 = 6/18, 6 es media proporcional de 2 y 18, y 2 y 18 son tercias proporcionales de 6. | ||
| + | |||
| + | Las proporciones presentan numerosas propiedades, que ya fueron estudiadas por los griegos y aparecen en el Libro V de los Elementos de Euclides. Esta es la fundamental: | ||
| + | |||
| + | 1.En toda proporción, el producto de los medios es igual al producto de los extremos: | ||
| + | |||
| + | a/b = c/d a *d = b*c | ||
| + | |||
| + | De aquí se desprende que un extremo es igual al producto de los medios dividiendo entre el otro extremo, y que un medio es igual al producto de los extremos dividiendo entre el otro medio: | ||
| + | |||
| + | a = (b*c)/d b = (a*d)/c c = (a*d)/b d = (b*c)/a | ||
| + | |||
| + | La comprobación de estas igualdades es muy fácil; puede verificarse con cualquiera de los ejemplos anteriores. Pero lo interesante es “saber ver proporciones” en todo producto de la forma a x d = b x c, o en toda expresión que pueda reducirse a ella. | ||
| + | |||
| + | 2. De toda proporción a/b = c/d, o de su expresión equivalente a*d =b*c, pueden derivarse otras tres proporciones diferentes: | ||
| + | |||
| + | a/c = b/d b/a = d/c c/a = d/b | ||
| + | |||
| + | ==Algunas situaciones particulares referidas a razones y proporciones== | ||
| + | |||
| + | '''Las escalas''' | ||
| + | |||
| + | Las escalas aluden al conocido problema de representar algún objeto o parte de la realidad en un mapa, plano o dibujo, sin distorsionar las relaciones que guardan entre sí los elementos que componen la realidad que se representa. Cuando esta transformación se hace correctamente, se dice que el dibujo, mapa o plano está “hecho a escala” (las fotografías y las fotocopias reducidas o ampliadas son ejemplos de reproducciones automáticas a escala).Hacerlo correctamente significa que se conservan, en el papel, las relaciones multiplicativas presentes en el objeto. Así, si un elemento A de la realidad mide la mitad de otro B, esa misma relación multiplicativa debe mantenerse en el papel. Indudablemente, estamos hablando de razones. Para conseguir una representación válida resulta clave hallar la escala o razón que existe entre la longitud de un determinado segmento del dibujo, plano o mapa, y la longitud del segmento correspondiente en la realidad representada. | ||
| + | |||
| + | Por ejemplo, si se dibuja el plano de una vivienda de tal modo que una distancia real de 10 metros se reduce a 2,5 cm en el plano, la escala utilizada es 2,5 cm : 10 m = 25 mm :10.000 mm = 1 : 400 (habitualmente, el primer término de la escala suele ser 1). Esto significa que cualquier medida sobre el plano debe multiplicarse por 400 en la realidad, y que cualquier medida en la realidad debe dividirse entre 400 para dibujarla en el plano. | ||
| + | |||
| + | '''Los repartos proporcionales''' | ||
| + | |||
| + | Se trata del tipo de situación en la que hay que repartir una cantidad de alguna magnitud entre diversos sujetos, de acuerdo con ciertas razones establecidas entre éstos. Por ejemplo, si se desea repartir una ganancia de 120.000 pesos entre dos socios cuyos aportes al capital están en razón de 3 a 5, la situación puede resolverse mediante la proporción siguiente: si y y z representan, respectivamente, las cantidades a percibir por cada socio, tenemos: y/z = 3/5, con el dato adicional: y + z = 120.000. Haciendo uso de la propiedad 5 de las proporciones: | ||
| + | |||
| + | Si a/b = c/d , entonces (a+b)/b = (c+d)/d y (a+b)/a = (c+d)/d | ||
| + | |||
| + | Cuando se trata de repartir proporcionalmente una cantidad N entre dos elementos que se hallan en una razón a/b, la cantidad percibida por el primer elemento es: (N*a)/(a+b) ; y la percibida por el segundo es: (N*b)/(a+b) .Este proceso puede generalizarse al caso en que haya más de dos elementos en el reparto proporcional. | ||
==Proporcionalidad Directa== | ==Proporcionalidad Directa== | ||
Revisión del 12:39 30 nov 2016
| ||||||
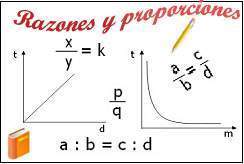
Razones y proporciones: Cuando son comparados dos números mediante una división diremos que esos dos números se encuentran en una razón; y si igualamos dos razones estamos en presencia de una proporción.
Sumario
Razón entre números
Al realizar una encuesta entre los jóvenes entre 18 y 21 años se concluye que: "1 de cada 5 jóvenes está inscrito en el Registro Electoral". Entonces, se puede decir que la razón entre los que votan y el total de jóvenes es 1: 5. También se puede decir que la razón entre los que votan y los que no, es 1: 4.
Sean a y b dos números racionales y b ‡ 0, entonces una razón entre a y b es el cociente a: b = a/b y lo leeremos a es a b.
Como las razones son números racionales, entonces se puede ampliarla y simplificarla como se desee mientras se mantenga la razón.
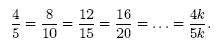
Una de las situaciones matemáticas más frecuente es sin duda, la de relacionar dos cantidades: se han hecho al sumarlas y restarlas, o al multiplicarlas y dividirlas. En particular, al relacionarlas mediante la resta y la división, estamos comparándolas. Existen dos tipos de comparaciones entre números: las que nos permiten averiguar cuál es el mayor calculando la diferencia existente entre ambos, o bien, calculando cuántas veces el mayor contiene al menor. En la primera situación hablamos de comparaciones o relaciones aditivas y en la segunda, de relaciones multiplicativas.
El concepto matemático de razón
Una razón es una relación multiplicativa entre dos números naturales diferentes de 0.
Hablamos así de la razón “dos a tres”,“1 a 10”, “7 a 4”, etc. Por ejemplo, si en un grupo de personas hay 18 hombres y 27 mujeres, diremos que la razón entre el número de hombres y el de mujeres es de “2 a 3”, es decir, que “hay 2 hombres por cada 3 mujeres”. En este caso, la razón entre el número de mujeres y el de hombres es la inversa, de “3 a 2”, es decir, que “hay 3 mujeres por cada 2 hombres”. Hay que saber distinguir entre los conceptos de razón y de fracción. Este último alude a la relación también multiplicativa entre la parte y el todo respectivo. En el ejemplo anterior, 2/5 representa la fracción ya simplificada correspondiente al número de hombres (18) con respecto al total de personas presentes (18 + 27 = 45). En el concepto de razón no está presente esta relación de carácter parte-todo.
Proporciones
La igualdad entre dos razones es una proporción.
Se lee:
- a es a b como c es a d.
- También puede escribirse a: b = c: d
- En toda proporción se tiene:
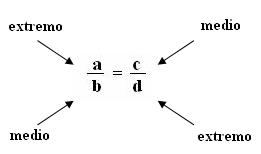
En toda proporción el producto de los extremos es igual al producto de los medios, esta relación se conoce como Teorema fundamental de la proporción, es decir.
Un ejemplo de proporción es 2/3 = 4/6, cuya lectura es “2 es a 3 como 4 es a 6”. De nuevo hay que recordar la distinción entre razones y fracciones, para no ver en la expresión anterior “la equivalencia de dos fracciones” (que será la lectura correcta cuando se hable de fracciones, pero no ahora...).
Vamos con la nomenclatura relativa a las proporciones. El uso de la notación a : b : :c : d nos ayuda a identificar a los números a y d como los extremos de la proporción y a los números b y c como los medios de la proporción. Por ejemplo, en 2/3 = 4/6, 2 y 6 son los extremos de la proporción, y 3 y 4, los medios.
Una proporción cuyos extremos y medios son diferentes se denomina discreta; por ejemplo, la anterior. Y continua, si los medios(o los extremos) son iguales entre sí; su forma sería: a/b = b/c ó a/b = c/a. Por ejemplo, 2/6 =6/18. En una proporción discreta, cualquier término se denomina cuarta proporcional de los otros tres. Así, en el ejemplo 2/3 = 4/6 decimos que 3 es cuarta proporcional de 2,4 y 6, ó que 4 lo es de 2, 3 y 6. En una proporción continua, el término repetido se denomina media proporcional de los otros dos, y estos dos últimos, tercia proporcional del otro término. Así, en el ejemplo 2/6 = 6/18, 6 es media proporcional de 2 y 18, y 2 y 18 son tercias proporcionales de 6.
Las proporciones presentan numerosas propiedades, que ya fueron estudiadas por los griegos y aparecen en el Libro V de los Elementos de Euclides. Esta es la fundamental:
1.En toda proporción, el producto de los medios es igual al producto de los extremos:
a/b = c/d a *d = b*c
De aquí se desprende que un extremo es igual al producto de los medios dividiendo entre el otro extremo, y que un medio es igual al producto de los extremos dividiendo entre el otro medio:
a = (b*c)/d b = (a*d)/c c = (a*d)/b d = (b*c)/a
La comprobación de estas igualdades es muy fácil; puede verificarse con cualquiera de los ejemplos anteriores. Pero lo interesante es “saber ver proporciones” en todo producto de la forma a x d = b x c, o en toda expresión que pueda reducirse a ella.
2. De toda proporción a/b = c/d, o de su expresión equivalente a*d =b*c, pueden derivarse otras tres proporciones diferentes:
a/c = b/d b/a = d/c c/a = d/b
Algunas situaciones particulares referidas a razones y proporciones
Las escalas
Las escalas aluden al conocido problema de representar algún objeto o parte de la realidad en un mapa, plano o dibujo, sin distorsionar las relaciones que guardan entre sí los elementos que componen la realidad que se representa. Cuando esta transformación se hace correctamente, se dice que el dibujo, mapa o plano está “hecho a escala” (las fotografías y las fotocopias reducidas o ampliadas son ejemplos de reproducciones automáticas a escala).Hacerlo correctamente significa que se conservan, en el papel, las relaciones multiplicativas presentes en el objeto. Así, si un elemento A de la realidad mide la mitad de otro B, esa misma relación multiplicativa debe mantenerse en el papel. Indudablemente, estamos hablando de razones. Para conseguir una representación válida resulta clave hallar la escala o razón que existe entre la longitud de un determinado segmento del dibujo, plano o mapa, y la longitud del segmento correspondiente en la realidad representada.
Por ejemplo, si se dibuja el plano de una vivienda de tal modo que una distancia real de 10 metros se reduce a 2,5 cm en el plano, la escala utilizada es 2,5 cm : 10 m = 25 mm :10.000 mm = 1 : 400 (habitualmente, el primer término de la escala suele ser 1). Esto significa que cualquier medida sobre el plano debe multiplicarse por 400 en la realidad, y que cualquier medida en la realidad debe dividirse entre 400 para dibujarla en el plano.
Los repartos proporcionales
Se trata del tipo de situación en la que hay que repartir una cantidad de alguna magnitud entre diversos sujetos, de acuerdo con ciertas razones establecidas entre éstos. Por ejemplo, si se desea repartir una ganancia de 120.000 pesos entre dos socios cuyos aportes al capital están en razón de 3 a 5, la situación puede resolverse mediante la proporción siguiente: si y y z representan, respectivamente, las cantidades a percibir por cada socio, tenemos: y/z = 3/5, con el dato adicional: y + z = 120.000. Haciendo uso de la propiedad 5 de las proporciones:
Si a/b = c/d , entonces (a+b)/b = (c+d)/d y (a+b)/a = (c+d)/d
Cuando se trata de repartir proporcionalmente una cantidad N entre dos elementos que se hallan en una razón a/b, la cantidad percibida por el primer elemento es: (N*a)/(a+b) ; y la percibida por el segundo es: (N*b)/(a+b) .Este proceso puede generalizarse al caso en que haya más de dos elementos en el reparto proporcional.
Proporcionalidad Directa
Supongamos que vamos por la carretera en un automóvil hacia una ciudad A, a una velocidad de 120 Km./h. Se puede reconocer 2 variables asociadas a esto: la distancia y el tiempo. Mientras más tiempo haya transcurrido, más distancia habremos recorrido, es decir, a medida que aumenta el tiempo, aumenta la distancia. De la misma manera, el tiempo que falta para llegar disminuye a medida que disminuye la distancia entre nosotros y la ciudad A.
Esta relación se conoce como proporcionalidad directa, si una variable aumenta o disminuye, entonces la otra variable también aumentará o disminuirá en la misma proporción.
La clave de una proporcionalidad directa, es que la razón entre ambas variables se mantenga constante. Este valor que se mantiene igual, independiente de como cambien las variables, se conoce como constante de proporcionalidad. En el ejemplo del viaje, la constante es igual a 120.
Para analizar la dicha proporcionalidad se lleva a una tabla las correspondientes variables, si en la medida que aumenta (disminuye) una variable la otra aumenta (disminuye) estamos en presencia de una proporcionalidad directa.
En el ejemplo anterior, las variables distancia recorrida y el tiempo recorrido lo se lleva a una tabla y se observa que en la medida que aumenta la distancia recorrida aumenta el tiempo.
El gráfico que representa a una proporcionalidad directa es una línea recta que pasa por el origen.
Proporcionalidad Inversa
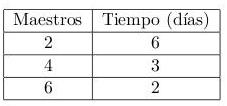
Supongamos que queremos pintar una casa y para ello contratamos 2 obreros. Ellos estiman que podrán pintar la casa completamente en 6 días.
Como el tiempo no nos pareció adecuado, entonces decidimos contratar 2 obreros más (4 en total) y estiman que podrán pintar la casa en 3 días.
Y como aún no nos parece suficiente, contratamos otros 2 obreros (6 en total) que estiman, podrán pintar toda la casa en 2 días lo cual nos parece bien. Podemos reconocer 2 variables asociadas a esto: los obreros y el tiempo. Claramente, mientras más obreros contratemos, menos tiempo demoraran.
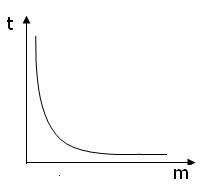
Esta relación se conoce como proporcionalidad inversa, si una variable aumenta (disminuye), entonces la otra variable disminuye (aumenta) en la misma proporción.
La clave de una proporcionalidad inversa, es que el producto entre ambas variables se mantenga constante. En el ejemplo de la casa, la constante es igual a 12.
De manera similar para analizar este tipo de proporcionalidad se lleva a una tabla las correspondientes variables, si en la medida que aumenta (disminuye) una variable la otra disminuye (aumenta) estamos en presencia de una proporcionalidad inversa.
En el ejemplo anterior, las variables obreros contratados y el tiempo que demoraran lo llevamos a una tabla y observamos que en la medida que aumenta la cantidad de obreros contratados disminuye el tiempo que demoraran.
En resumen, si x e y son dos variables que se encuentran en
- Proporcionalidad Directa, entonces se cumple que
Archivo:Relacion prop directa.JPG
- Proporcionalidad Inversa, entonces se cumple que
Archivo:Relacion prop inversa.JPG
Donde k es la constante de proporcionalidad respectiva.
Fuentes
- Libro de texto. Matemática 6to grado
- Libro de texto. Matemática 9no grado