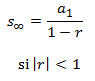Sucesión (matemática)
| ||||||
Sucesión. En matemáticas, una sucesión o progresión es un conjunto ordenado de números. Cada uno de los números que conforma la sucesión se denomina término n-ésimo, siendo n la posición de cada término.
Sumario
Ejemplos
- Sucesión de los números pares (positivos): 0, 2, 4, 6, 8, 10, 12,...
- Sucesión de los números impares (positivos): 1, 3, 5, 7, 9, 11, 13,...
- Sucesión de las potencias de dos: 2, 4, 8, 16, 32, 64,...
Tipos de sucesiones
Se distinguen principalmente dos tipos de sucesiones:
- Aritmética: cada término de la sucesión se obtiene al sumar una constante al término anterior. Esta constante se denomina diferencia.
- Geométrica: cada término de la sucesión se obtiene al multiplicar por el término anterior por una constante. Esta constante se denomina razón.
- Recursiva: la definición de la sucesión se define por recursión (véase el término general de la sucesión de Fibonacci en Ejemplos).
Ejemplos
- Las sucesiones de los números pares (0, 2, 4, 6, 8,...) y la de los números impares (1, 3, 5, 7,...) son aritméticas con diferencia d = 2.
- La sucesión de las potencias de dos (2, 4, 8, 16, 32,...) es geométrica con razón r = 2.
- La sucesión 2, 1, 0.5, 0.25, 0.125, 0.0625... es geométrica con razón r = 0.5.
- La sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21,...) es recursiva. Cada término se obtiene sumando los dos que le preceden, excepto los dos primeros términos que son, por definición, 1.
sucesiones por la cantidad
- finita
cuando tiene n términos exactos
- lunes, martes, miércoles, jueves, viernes, sábado y domingo
- u0 , u1 , u2 ,u3 , u4 , todas las raíces quinras generadas por una raíz quinta primitiva de 1.
- infinita
cuando no es finita
- 4, 7, 10, 13,...3n+1,...
Monotonía de una sucesión
Una sucesión es
- monótona creciente cuando cada término es mayor o igual que el anterior: an ≤ an + 1.
- monótona decreciente cuando cada término es menor o igual que el anterior: an ≥ an + 1
Si los signos de desigualdad son estrictos ("<" o ">"), se dice que la monotonía es estricta.
- Las sucesiones de los números pares (0, 2, 4, 6, 8,...) y la de los números impares (1, 3, 5, 7,...) son estrictamente monótonas crecientes.
- La sucesión 2, 1, 0.5, 0.25, 0.125, 0.0625... es estrictamente monótona decreciente.
Diferencia y razón
- La diferencia de una sucesión aritmética es la diferencia entre dos términos consecutivos: d = an + 1 - an.
- La razón de una sucesión aritmética es la razón entre dos términos consecutivos: d = an + 1/an.
Término general
El término general de una sucesión es la fórmula en función de n que permite obtener el término n-ésimo de la sucesión sin necesidad de conocer todos los otros términos.
- En una sucesión aritmética con diferencia d y primer término a1, el término general es an = a1 + (n-1)·d.
- En una sucesión geométrica con razón r y primer término a1, el término general es an = a1·rn - 1.
Ejemplos
- El término general de la sucesión de los números pares (0, 2, 4, 6, 8,...) es an = 2(n-1).
- El término general de la sucesión de los números impares (1, 3, 5, 7,...) es an =1 + 2(n-1).
- El término general de la sucesión de las potencias de dos (2, 4, 8, 16, 32,...) es an = 2n.
- El término general de la sucesión geométrica 2, 1, 0.5, 0.25, 0.125, 0.0625... es an = 2·0.5n - 1.
- El término general de la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21,...) es an + 2 =an + an + 1.
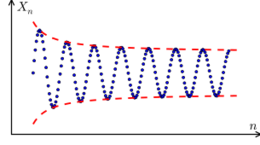
Convergencia
Una sucesión an es convergente si existe el límite de an cuando n tiende a infinito. Si no, se dice que es divergente.[1]
Ejemplos
- Las sucesiones de los números pares (0, 2, 4, 6, 8,...) y la de los números impares (1, 3, 5, 7,...) son divergentes.
- La sucesión 2, 1, 0.5, 0.25, 0.125, 0.0625... es convergente a 0.
Suma de términos
Existe una fórmula para calcular la suma de los n primeros términos de una sucesión:
- si es aritmética con diferencia d,
- si es geométrica con razón r,
Además, en las sucesiones geométricas con razón r tal que |r| < 1, la suma de infinitos términos de la sucesión es finita y puede calcular mediante la fórmula
Véase también
Fuentes
- Progresiones: problemas resueltos (Matesfacil.com)
- Introducción a las progresiones (Problemasyecuaciones.com)