Topología
| ||||||
Topología. La más joven de las ramas clásicas de las Matemáticas. En contraste con el Álgebra, la Geometría y la Teoría de los números, cuyas genealogías datan de tiempos antiguos, la topología aparece en el siglo diecisiete, con el nombre de analysis situs, esto es, análisis de la posición.
"La Topología es Matemática cualitativa , es decir matemática sin números. Podemos decir a grosso modo , que la Topología trata de las propiedades intrínsecas de las configuraciones espaciales , que son independientes del tamaño, la situación y la forma...Una propiedad cualitativa intrínseca es aquella que no cambia cuando el objeto que se está considerando sufre un proceso de dilatación y flexión sin ruptura " [1]
Sumario
Historia
Los conceptos de adyacencia , entorno, de lo infinitamente cercano, de igual modo el concepto de disección de un cuerpo, hasta cierto punto intercambiable con los conceptos anteriores, son los que Lobachevski ubica en el sustento de toda la armazón de la geometría y son además , los conceptos liminares, en síntesis , los conceptos fundamentales de la Topología en toda la amplitud en que se entiende actualmente esta disciplina. [2]
Como anticipo del origen de la Topología debe tomarse la definición clásica de la continuidad. Cuanto más esté x cerca de a tanto más próximo de l estará g(a). Propuesta clara enunciada por el matemático galo, Luis Cauchy, en 1821. Fecha que marcó, por este caso y otros conceptos introducidos por él, un cambio revolucionario en la matemática, lo que propició el desarrollo del proceso que ha llevado al sitio de la enorme expansión y aplicación actuales. [3]
Los inicios de la Topología se hallan en en la obra de Carlos Weirstrass, por 1860, en la que analizó el concepto de límite de una función - tal como se emplea en el cálculo. En este esfuerzo rearmó el sistema de números reales y transparentó algunas de sus características ahora nombradas "topológicas". A continuación el mayúsculo aporte fundacional de Jorge Cantor, miembro de la Academia de Ciencias de San Peterburgo (Rusia) sobre la teoría de conjuntos de puntos ( 1874-1895), fija los fundamentos sobre los cuales la Topología construiría circunstancialmente su propio andamiaje. Un segundo matiz de la Topología, llamado topología algebraica o combinatoria empezó en 1890 con el destacado trabajo de Enrique Poincaré sobre la teoría del cálculo integral en espacios polidimensionales. F. Hausdorff y otros, en el lapso de de 1900 -1910, establecieron sólidos basamentos para el primer matiz topológico, que no es sino la nombrada topología conjuntista. L.E. J. Brouwer, en su indagación (1908-1912) del concepto de dimensión, fue el pionero en tratar una mixtura de carices conjuntistas y combinatorios de la Topología. La teoría integrada experimentó un gran ritmo expansivo, en el lapso de 1915 a 1930, como fruto de los esfuerzos de los matemáticos J. W. Alexander, P.L. Alexandrov, Salomón Lefschetz y otros. Hasta 1930 la Topología era llamada como análisis in situ. Fue Lefschetz el autor primigenio y popularizador del vocablo topología, habiendo sacado a luz un tratado con tal título en 1930. Término onomático de aceptación universal.
Desde la fecha onomástica
A partir de esta fecha - 1930- la Topología se ha desarrollado a un ritmo casi exponencial. Esta disciplina incursionó en el cálculo de variaciones por medio de la teoría de puntos críticos forjada por el matemático estodounidense, M. Morse. Se da un impulso nuevo a la geometría diferencial por el trabajo de H. Whitney. Concretamente, sobre paquetes fibrados, el trabajo de G. de Rham y el de grupos de Lie de H. Hope abren nuevas perspectivas. Se efectuó una revolución menor en el álgebra moderna con el despliegue de nuevos sustentos para el Álgebra y una nueva rama, conocida como álgebra homológica. Mucha contribución debe este producto a S. Eilenberg y a S. Mac Lane . La topología dio un nuevo empuje a la geometría algebraica a través de la teoría de haces y cohomología y produjo nuevas e importantes aplicaciones en la teoría de ecuaciones en derivadas parciales en base a los trabajos de J. Leray y M. Atiyah. La influencia de la Topología en la geometría diferencial ha iniciado el pensamiento topológico en teoría de la relatividad. La Topología ha alcanzado a ser una disciplina básica de las Matemáticas, en la práctica, una necesidad en algunas materias ( un curso de Análisis matemático supone una introducción sobre concepto de vecindad y abiertos, por decir, o en teoría de grafos) . Ante todo, una energía integradora para casi todas las Matemáticas ( destacada en la orientación bourbakista).
Características
La topología es una rama de las matemáticas que estudia la continuidad y otros conceptos originados a partir de ella. Se trata de una especialización vinculada a las propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas, con independencia de su tamaño o forma. Las funciones continuas de la matemática son aquellas que, en los puntos cercanos del dominio, sufren pequeñas variaciones en los valores. A nivel gráfico, estas funciones suelen estar en condiciones de dibujarse sin necesidad de levantar el lápiz del papel. Otro concepto central de la topología es el espacio topológico, que es una estructura matemática que permite la definición formal de continuidad, conectividad y convergencia, entre otros conceptos.
La topología, por lo tanto, es la especialización que estudia las funciones continuas y los espacios topológicos. Esta disciplina trabaja con los objetos de distintas formas, siempre que no se interrumpa la mencionada continuidad. En palabras del lenguaje cotidiano, podría decirse que la topología tiene permitido doblar, estirar, retorcer o achicar los objetos, pero sin romperlos o separando aquello que estaba unido (ni pegando lo que estaba separado). A nivel topológico, un triángulo es lo mismo que una circunferencia: uno puede ser transformado en el otro de manera continua, sin necesidad de cortar o pegar. En cambio, una circunferencia nunca puede ser transformada en un segmento desde el punto de vista topológico, ya que dicha transformación requeriría de romper la continuidad de la figura. Entre las ramas de la topología, es posible distinguir entre la topología general (también llamada topología conjuntista), la topología diferencial y la topología algebraica.
Tipos de topología
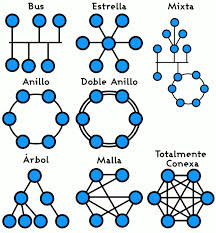
La topología define la estructura de una red. La definición de topología está compuesta por dos partes, la topología física, que es la disposición real de los cables (los medios) y la topología lógica, que define la forma en que los hosts acceden a los medios. Las topologías físicas que se utilizan comúnmente son de bus, de anillo, en estrella, en estrella extendida, jerárquica y en malla.
Topología de anillo
Una topología de anillo se compone de un solo anillo cerrado formado por nodos y enlaces, en el que cada nodo está conectado solamente con los dos nodos adyacentes.
Los dispositivos se conectan directamente entre sí por medio de cables en lo que se denomina una cadena margarita. Para que la información pueda circular, cada estación debe transferir la información a la estación adyacente (todas la host estan conectadas una con la otra formando una cadena de circuito cerrado.)
Topología de estrella
Tiene un nodo central desde el que se irradian todos los enlaces hacia los demás nodos. Por el nodo central, generalmente ocupado por un hub, pasa toda la información que circula por la red. La ventaja principal es que permite que todos los nodos se comuniquen entre sí de manera conveniente. La desventaja principal es que si el nodo central falla, toda la red se desconecta.
Topología bus
La topología de bus tiene todos sus nodos conectados directamente a un enlace y no tiene ninguna otra conexión entre nodos. Físicamente cada host está conectado a un cable común, por lo que se pueden comunicar directamente, aunque la ruptura del cable hace que los hosts queden desconectados. La topología de bus permite que todos los dispositivos de la red puedan ver todas las señales de todos los demás dispositivos, lo que puede ser ventajoso si desea que todos los dispositivos obtengan esta información. Sin embargo, puede representar una desventaja, ya que es común que se produzcan problemas de tráfico y colisiones, que se pueden paliar segmentando la red en varias partes. Es la topología más común en pequeñas LAN, con hub o switch. final en uno de los extremos.
Topología malla
Cada nodo se enlaza directamente con los demás nodos. Las ventajas son que, como cada todo se conecta físicamente a los demás, creando una conexión redundante, si algún enlace deja de funcionar la información puede circular a través de cualquier cantidad de enlaces hasta llegar a destino. Además, esta topología permite que la información circule por varias rutas a través de la red. La desventaja física principal es que sólo funciona con una pequeña cantidad de nodos, ya que de lo contrario la cantidad de medios necesarios para los enlaces, y la cantidad de conexiones con los enlaces se torna abrumadora.
Referencias
- ↑ M.J. Mansfield. Introducción a la Topología. Editorial Alhambra , Madrid, 1974. ISBN 84-205-0450-5
- ↑ A. .D. Aleksandrov, A.N. Kolmogorov, M.A. Laurentiev y otros. La matemática: su contenido, métodos y significado. Alianza Universidad, Madrid, 1982. ISBN 84-206-2070-X tomo iii
- ↑ José Tola P. Introducción a la Topología. PUCP Fondo Editorial -1992- Lima.
Literatura consultable
- Munkres. Topología.Pearson- Prentice Hall- 2008- ISBN 978-84-205-3180-9
- Ayala- Domínguez-Quintero- Elementos de la topología general. Addison- Wesley Iberoamericana- ISBN 84-78-29-006-0
- W.gG. Chinn, N.E.Steenrod. Primeros conceptos de topología. Editorial Alhambra, Madrid, 1975-ISBN 84-205-0524-2
Fuentes
- Topología. Visitado el 16 de abril de 2012.
- Definición. Visitado el 16 de abril de 2012.
- Tipos de topología. Visitado el 16 de abril de 2012.
- Topologías. Visitado el 16 de abril de 2012.