Cálculo de circuitos simétricos trifásicos
| ||||||
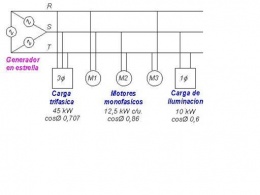
Cálculo en circuitos simétricos trifásicos. En los circuitos eléctricos trifásicos los elementos se interconectan formando una delta o una estrella e incluso hay elementos que se conectan a una sola fase, llamándose en este caso monofásicos.
Aquí se verá el cálculo de corrientes en el circuito trifásico simétrico de la Fig. 1. En el mismo la fuente está conectada en delta. A este circuito se conectan dos cargas: elementos 2 y 4; la primera de las cuales se conecta en estrella y la segunda en delta. Los elementos 1 y 3 simbolizan las impedancias en las líneas.
Sumario
Transformaciones en el circuito
Se asume que los voltajes en los terminales de la fuente son simétricos y conocidos y que las resistencias del circuito, elementos 1, 2, 3 y 4, también son conocidos. Para simplificar los cálculos, los circuitos en delta de la fuente y de la carga 4 se transformarán en circuitos en estrella.
- Las resistencias de fase de un circuito en estrella simétrica son un tercio de las resistencias de fase en un circuito en delta simétrica equivalente.
- Los voltajes de fase de la estrella equivalente de la fuente son 1/√3 de veces menores que los voltajes de la línea originales.
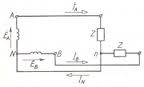
El circuito transformado se muestra en la Fig. 2.
En un circuito simétrico, los puntos neutros (N y n) están al mismo potencial[1]. Por consiguiente, sin modificar las condiciones del circuito, estos se pueden conectar entre si, a través de un conductor sin resistencia (tal como el indicado por la línea punteada en el diagrama).
Circuito equivalente
Ahora se eliminarán dos fases del circuito, por ejemplo B y C, para obtener el circuito de la Fig. 3. Estas manipulaciones no afectan las condiciones en la fase restante (A). Como se ve, las ecuaciones escritas según las leyes de Kirchhoff para el nodo A' y los lazos A-A'-n1-N y A'-n2-n1-A ' en los circuitos de las Fig. 2 y 3 serán iguales. Dicho de otra forma, las corrientes y voltajes en las fases son los mismos en ambos circuitos.
Los circuitos trifásicos simétricos, compuestos de múltiples mallas, son resueltos utilizando modelos monofásicos. La corriente en la fase A puede ser calculada a partir del circuito equivalente monofásico de la Fig. 3. Incluso, se puede reemplazar la conexión paralela de las ramas A’-n2 y A'-n2 y A'-n1 por un resistencia equivalente. Las corrientes en las fases B y C son iguales en magnitud a la corriente en la fase A. Las corrientes en el las ramas del circuito en delta (4) son 1/√3 veces mayores que en las impedancias en las líneas (3). Para cada uno de los elementos (1, 2, 3 y 4), la corriente está desplazada en fase con respecto a la corriente en los propios componentes del mismo elemento, en ±120°.
Conclusiones
- Los circuitos trifásicos simétricos, compuestos de múltiples mallas, son resueltos utilizando modelos monofásicos, lo que garantiza una gran simplificación en los cálculos.
- Para obtener los circuitos equivalentes solo hay que tener en cuenta las interrelaciones que existen para obtener una delta de una estrella y viceversa.
Véase también
Fuentes
- Ayllón Fandiño, E. (1987). Fundamentos de la teoría de los circuitos eléctricos II. La Habana: Pueblo y Educación.
- Bessonov, L. A. (1984). Teoreticheskie osnovi electrotejniki. Moscú: Vysshaia shcola.
- Evdokimov, F. E. (1981). Teoreticheskie osnovi electrotejniki. Moscú: Vysshaia shcola.
- Kasatkin, A. S., Nemtsov, M. V. (1983). Electrotejnika. Moscú: Energoatomizdat.
- Kerchner, R. M., Corcoran, G .F. (1975). Circuitos de corriente alterna. La Habana: Pueblo y educación.
- Leyes o (Lemas) de Kirchhoff. (2011). Retrieved 28/04/2011, 2011, from [1]
- Neiman, L. R., Demirchian, L. R. (1981). Teoreticheskie osnovi electrotejniki. Leningrado: Energoizdat.
- Zeveke, G. V. (1979). Analysis and synthesis of electric circuits. Moscú: Mir.