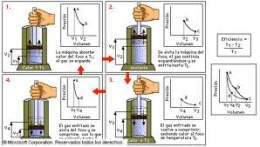
Ciclo de Carnot
| ||||||
Ciclo de Carnot. Ciclo termodinámico hipotético utilizado como norma para establecer comparaciones con ciclos reales. Con el ciclo de Carnot se muestra que, aun en condiciones ideales, una máquina térmica no puede convertir toda la energía calorífica que se le suministra en energía mecánica; tiene que rechazar parte de esa energía.
En un ciclo de Carnot, una máquina acepta energía calorífica de una fuente a alta temperatura, o cuerpo caliente, convierte parte de ella en trabajo mecánico (o eléctrico) y descarga el resto hacia un sumidero a baja temperatura, o cuerpo frío. Cuanto mayor sea la diferencia en temperatura entre la fuente y el sumidero, mayor será la eficiencia de la máquina térmica.
Sumario
Características generales
El ciclo de Carnot consiste, primero, en una compresión isoentrópica, luego, en una adición isotérmica de calor, seguida de una expansión isoentrópica, y concluye con un proceso isotérmico de rechazo de calor. En pocas palabras, los procesos son compresión, adición de calor, expansión y descarga del calor, todo en una forma establecida y definida. El efecto neto del ciclo es que se agrega calor a una alta temperatura constante, se descarga algo menos de calor a una temperatura baja constante, y la suma algebraica de estas cantidades de calor es igual al trabajo efectuado por el ciclo.
Un ciclo de Carnot consta, en su totalidad, de procesos breversibles; así, en teoría, puede aplicarse para extraer el calor de un cuerpo frío y descargarlo a un cuerpo caliente. Para ello, el ciclo requiere entrada de trabajo de sus alrededores. El equivalente de calor de esta entrada de trabajo también se descarga al cuerpo caliente. Así como el ciclo de Carnot produce la máxima eficiencia para un ciclo de potencia que funciona entre dos temperaturas fijas, el ciclo inverso produce el óptimo coeficiente de rendimiento para un aparato que bombee calor desde una temperatura baja hasta una más alta.
Pese a las ventajas que tiene el ciclo de Carnot, serias dificultades surgen cuando se desea construir una máquina real de Carnot. Las presiones y temperaturas pico necesariamente altas limitan la eficiencia térmica práctica que puede lograrse en una máquina real. Aunque el ciclo de Carnot es independiente de la sustancia de trabajo y, por ello, es aplicable a un ciclo de vapor, la dificultad para la compresión eficiente de una mezcla vapor-líquido lo hace impráctico.
Rendimiento
El rendimiento viene definido, como en todo ciclo, por
![]() y, como se verá adelante, es mayor que cualquier máquina que funcione cíclicamente entre las mismas fuentes de temperatura. Una máquina térmica que realiza este ciclo se denomina máquina de Carnot.
y, como se verá adelante, es mayor que cualquier máquina que funcione cíclicamente entre las mismas fuentes de temperatura. Una máquina térmica que realiza este ciclo se denomina máquina de Carnot.
Como todos los procesos que tienen lugar en el ciclo ideal son reversibles, el ciclo puede invertirse. Entonces la máquina absorbe calor de la fuente fría y cede calor a la fuente caliente, teniendo que suministrar trabajo a la máquina. Si el objetivo de esta máquina es extraer calor de la fuente fría se denomina máquina frigorífica, y si es aportar calor a la fuente caliente, bomba de calor.
Etapas
El ciclo de Carnot consta de cuatro etapas: dos procesos isotermos (a temperatura constante) y dos adiabáticos (aislados térmicamente). Las aplicaciones del Primer principio de la termodinámica están escritos acorde con el Criterio de signos termodinámico.
Expansión isoterma: (proceso 1 ? 2 en el diagrama) Se parte de una situación en que el gas se encuentra al mínimo volumen del ciclo y a temperatura T1 de la fuente caliente. En este estado se transfiere calor al cilindro desde la fuente de temperatura T1, haciendo que el gas se expanda. Al expandirse, el gas tiende a enfriarse, pero absorbe calor de T1 y mantiene su temperatura constante. Al tratarse de un gas ideal, al no cambiar la temperatura tampoco lo hace su energía interna, y despreciando los cambios en la energía potencial y la cinética, a partir de la 1ª ley de la termodinámica vemos que todo el calor transferido es convertido en trabajo:
Desde el punto de vista de la entropía, ésta aumenta en este proceso: por definición, una variación de entropía viene dada por el cociente entre el calor transferido y la temperatura de la fuente en un proceso reversible:
Como el proceso es efectivamente reversible, la entropía aumentará.
Expansión adiabática: (2 ? 3) La expansión isoterma termina en un punto tal que el resto de la expansión pueda realizarse sin intercambio de calor. A partir de aquí el sistema se aísla térmicamente, con lo que no hay transferencia de calor con el exterior. Esta expansión adiabática hace que el gas se enfríe hasta alcanzar exactamente la temperatura T2 en el momento en que el gas alcanza su volumen máximo. Al enfriarse disminuye su energía interna, con lo que utilizando un razonamiento análogo al anterior proceso:
Compresión isoterma: (3 ? 4) Se pone en contacto con el sistema la fuente de calor de temperatura T2 y el gas comienza a comprimirse, pero no aumenta su temperatura porque va cediendo calor a la fuente fría. Al no cambiar la temperatura tampoco lo hace la energía interna, y la cesión de calor implica que hay que hacer un trabajo sobre el sistema:
Al ser el calor negativo, la entropía disminuye:
Compresión adiabática: (4 ? 1) Aislado térmicamente, el sistema evoluciona comprimiéndose y aumentando su temperatura hasta el estado inicial. La energía interna aumenta y el calor es nulo, habiendo que comunicar un trabajo al sistema:
Al ser un proceso adiabático, no hay transferencia de calor, por lo tanto la entropía no varía:
Signos
Por convención de signos, un signo negativo significa lo contrario. Es decir, un trabajo negativo significa que el trabajo es realizado sobre el sistema.
Con este convenio de signos el trabajo obtenido deberá ser, por lo tanto, negativo. Tal como está definido, y despreciando los cambios en energía mecánica, a partir de la primera ley:
Teoremas de Carnot
1. No puede existir una máquina térmica que funcionando entre dos fuentes térmicas dadas tenga mayor rendimiento que una de Carnot que funcione entre esas mismas fuentes térmicas.
Para demostrarlo supondremos que no se cumple el teorema, y se verá que el no cumplimiento transgrede la segunda ley de la termodinámica. Tenemos pues dos máquinas, una llamada X y otra, de Carnot, R, operando entre las mismas fuentes térmicas y absorbiendo el mismo calor de la caliente.
2. Dos máquinas reversibles operando entre las mismas fuentes térmicas tienen el mismo rendimiento.Igual que antes, suponemos que no se cumple el teorema y veremos que se violará el segundo principio. Sean R1 y R2 dos máquinas reversibles, operando entre las mismas fuentes térmicas y absorbiendo el mismo calor de la caliente, con distintos rendimientos
Rendimiento
A partir del segundo teorema de Carnot se puede decir que, como dos máquinas reversibles tienen el mismo rendimiento, este será independiente de la sustancia de trabajo de las máquinas, las propiedades o la forma en la que se realice el ciclo. Tan solo dependerá de las temperaturas de las fuentes entre las que trabaje. Si tenemos una máquina que trabaja entre fuentes a temperatura T1 y T2, el rendimiento será una función de las dos como variables:
Ciclo real
Todos los procesos reales tienen alguna irreversibilidad, ya sea mecánica por rozamiento, térmica o de otro tipo. Sin embargo, las irreversibilidades se pueden reducir, pudiéndose considerar reversible un proceso cuasiestático y sin efectos disipativos.
Los efectos disipativos se reducen minimizando el rozamiento entre las distintas partes del sistema y los gradientes de temperatura; el proceso es cuasiestático si la desviación del equilibrio termodinámico es a lo sumo infinitesimal, esto es, si el tiempo característico del proceso es mucho mayor que el tiempo de relajación (el tiempo que transcurre entre que se altera el equilibrio hasta que se recupera).
Por ejemplo, si la velocidad con la que se desplaza un émbolo es pequeña comparada con la del sonido del gas, se puede considerar que las propiedades son uniformes espacialmente, ya que el tiempo de relajación mecánico es del orden de V1/3/a (donde V es el volumen del cilindro y a la velocidad del sonido), tiempo de propagación de las ondas de presión, mucho más pequeño que el tiempo característico del proceso, V1/3/w (donde w es la velocidad del émbolo), y se pueden despreciar las irreversibilidades.
Si se hace que los procesos adiabáticos del ciclo sean lentos para minimizar las irreversibilidades se hace imposible frenar la transferencia de calor. Como las paredes reales del sistema no pueden ser completamente adiabáticas, el aislamiento térmico es imposible, sobre todo si el tiempo característico del proceso es largo. Además, en los procesos isotermos del ciclo existen irreversibilidades inherentes a la transferencia de calor. Por lo tanto, es imposible conseguir un ciclo real libre de irreversibilidades, y por el primer teorema de Carnot la eficiencia será menor que un ciclo ideal.
Fuentes
- Disponible en http://www.sc.ehu.es/sbweb/fisica/estadistica/carnot/carnot.htm
- Enciclopedia McGraw-Hill de Ciencia y Tecnología. 2da. Edición, Tomo II, 1992, pp.384