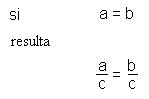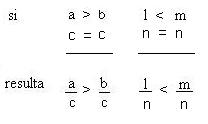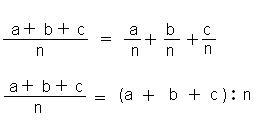División
| ||||||
División. Una de las operaciones básicas de la matemática. Procedimiento que se utiliza para repartir objetos entre personas.
Sumario
Concepto
La división es una operación aritmética que tiene por objeto, dados un producto de dos factores y uno de ellos, hallar el otro.
La división la operación inversa de la multiplicación. Es la única la operación inversa de la multiplicación, por ser esta una operación conmutativa.
Nomenclatura y notación
El producto conocido se llama dividendo; el factor conocido, divisor, y el factor que se busca, cociente. El dividendo y el divisor, conjuntamente, se llaman término de la división.
Llamando D al dividendo, d al divisor y c al cociente, podemos escribir que:
D: d = c
teniendo que ser, por la definición,
d x c = D
Es decir: El producto del divisor por el cociente es igual al dividendo.
De acuerdo con la definición, por ser c uno de los dos factores del producto D, resultará que:
D: c = d
O sea: El divisor es igual al dividendo partido por el cociente.
La operación de dividir puede indicarse en cualquiera de las siguientes formas, siendo a y b dos números cualesquiera. 
Otra forma, muy usual en nuestro país, de representar la división es utilizando la galera:
Nota: En la división es muy importante que siempre tengas en cuenta que divisor debe ser distinto de cero, pues la división por cero no se puede realizar. Sin embargo en dividendo sí puede ser cero. En este caso se cumple que 0 : a = 0.
Otras interpretaciones de la división
Puede considerarse que dividir un número entre otro es:
- Tratar de averiguar cuántas veces contiene el primero al segundo. Es decir que 36: 9 = 4 significa que el 36 contiene 4 veces al 9. En efecto: 9 + 9 + 9 + 9 = 36
- Una resta abreviada en la cual se trata de averiguar cuántas veces el divisor puede restarse del dividendo y las sucesivas diferencias. Según esto 36 : 9 = 4 significa que el 9 se puede restar 4 veces de 36. En efecto:
36 – 9 = 27; 27 – 9 = 18; 18 – 9 = 9 y 9 – 9 = 0
- Una repartición de objetos entre personas, en la cual el dividendo representa el número de objetos que se reparten y el divisor el número de personas entre quienes se reparte, representando el cociente el número de objetos que le corresponde a cada persona. Es decir que: 36 : 9 = 4 puede considerarse que significa que si se reparte 36 objetos entre 9 personas, le corresponde 4 objetos a cada persona.
Tipos de división. Cociente entero aproximado por defecto o por exceso.
Si el dividendo es múltiplos del divisor, la división se llama exacta.
Si el dividendo no es múltiplo del divisor, no podrá encontrase un números naturales que multiplicado por el divisor dé el dividendo. Es decir la división no es siempre posible dentro del campo de los números naturales.
Ejemplo: 25 : 7 no hay ningún números naturales que multiplicado por 7 dé 25, no podemos efectuar esta operación dentro del campo de esos números pero existen dos números consecutivos (3 y 4) tales que sí el divisor se multiplica por el menor el producto es menor que el dividendo, (3 x 7 = 21; no llega) y si se multiplica por el mayor el producto es mayor que el dividendo (4 x 7 = 28, se pasa) En este caso la división se llama división inexacta o entera. El cociente obtenido se llama cociente aproximado: por defecto si se toma el menor, por exceso si se toma el mayor de los dos números consecutivos, en este caso el cociente entero aproximado por defecto es 3 y por exceso es 4.
La diferencia entre el dividendo y el producto del divisor por el cociente se llama residuo o resto, que será por defecto o por exceso según lo sea el cociente aproximado.
Nota. Cuando se habla de cociente entero o de residuo, sin explicar de cual se trata, se hace referencia al cociente entero y al residuo por defecto.
Por lo tanto, en la división entera por defecto el dividendo es igual al producto del divisor por el cociente, más el residuo. Si llamamos r al residuo por defecto podremos escribir siempre que:
D = d x c + r
Por lo que para comprobar si una división está bien realizada, se multiplica el cociente por el divisor y se suma el resto; el resultado debe ser el dividendo.
Leyes de la división exacta.
Las leyes principales de la división exacta son:
1- Ley de la uniformidad:
• La división de números respectivamente iguales da siempre el mismo resultado, o
• Si los dos miembros de una igualdad se dividen por un mismo número, la igualdad subsiste. Es decir que:
• Si se dividen ordenadamente dos igualdades, resulta otra igualdad. Es decir que:
2- Ley de la monotonía:
• Si los dos miembros de una desigualdad se dividen por un mismo número, la desigualdad subsiste. Es decir que:
Si se dividen ordenadamente una desigualdad entre una igualdad, resulta una desigualdad del mismo sentido que la desigualdad dividendo. Es decir que:
Caso en que la desigualdad sea divisor.
Si se divide una igualdad entre una desigualdad, resulta una desigualdad de sentido contrario que la desigualdad divisor. Es decir que:
División de desigualdades: Si se dividen dos desigualdades de sentido contrario, resulta una desigualdad del mismo sentido que la desigualdad dividendo. Es decir:
Nota: Cuando se dividen dos desigualdades del mismo sentido, el resultado podrá se una desigualdad del mismo sentido o de sentido contrario, o una igualdad. Es decir que:
3-Ley distributiva
Ley distributiva de la división con respecto a la suma: Para dividir una suma indicada por un número se puede dividir cada sumando por dicho número y sumar los cocientes obtenidos o realizar primero la suma indicada y después dividir por dicho número. Es decir:
Ley distributiva de la división con respecto a la resta: Para dividir una diferencia indicada por un número se puede dividir el minuendo por dicho número y después el sustraendo, y restar este segundo cociente del anterior o restar primero y después efectuar la división.
Generalizando:
División de una suma algebraica por un número.
Para dividir una suma algebraica por un número, se puede dividir cada término por el número, escribiendo delante de cada cociente el signo del término que hizo de dividendo, y efectuando luego las sumas y restas indicadas o efectuar la suma algebraica y después dividir
Generalizando:

Fuentes
- Sócrates Rosell Franco. Aritmética. Volumen I. Segunda Edición.
- Microsoft Encarta. División “Aritmética”
- Libro de texto Quinto Grado.
Véase también