Función Kernel
Las Funciones Kernel. Son funciones matemáticas que se emplean en las Máquinas de Soporte Vectorial. Estas funciones son las que le permiten convertir lo que sería un problema de clasificación no lineal en el espacio dimensional original, a un sencillo problema de clasificación lineal en un espacio dimensional mayor.
Sumario
Trascendencia histórica
En 1951 Kuhn y Tucker generalizaron la teoría de Lagrange permitiéndose entonces la introducción de restricciones de desigualdad en los problemas de optimización en el que se utiliza el producto del punto, con funciones en el espacio de características que son llamadas Kernels.
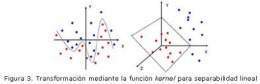
La minimización del Riesgo Empírico y la dimensión de Vapnik-Chervonenkis son fundamentales para lograr la búsqueda de la solución óptima mediante funciones que en un espacio numérico determinado, logre el hiperplano separador. En la representación de estos conjuntos de entrenamiento, los mismos pueden estar linealmente separados. De no ser así, se utilizan las funciones Kernels para llevar estas muestras a un plano de mayor dimensión donde puedan ser linealmente separables. Dentro de los más utilizados se encuentran: el Kernel Polinomial y el de Base Radial.
Kernels
Para que las funciones kernel puedan ser consideradas candidatas a kernels, deben cumplir tres condiciones iniciales fundamentales; deben ser:
- Continuas
- Simétricas
- Positivas.
Estos son los requerimientos básicos para poder ser expresadas como un producto escalar en un espacio dimensional alto. El espacio dimensional simulado mediante las funciones kernel se define tomando a cada característica de los datos como una dimensión. Esto convierte a las entradas en un conjunto de puntos en un espacio euclidiano n-dimensional. Es mucho más fácil establecer relaciones entre los datos expresados en esta forma.
Con el objetivo de identificar los kernels óptimos a incorporar se analizan numerosas opciones disponibles, entre las posibilidades destacan los siguientes kernels: Gaussiano, Fisher, String y Hubert de anchura modificada. Algunos de los anteriores kernels llegaron hasta la fase de implementación y prueba. No obstante se trabaja sobre una familia de kernels muy vinculada a la teoría de algoritmos ensemble infinitos.
Tipos de Kernel
Stump kernel
Es un kernel que encarna un número infinito de decisiones stump. La decisión stump es uno de los modelos de aprendizaje base más simples que se aplican, se trata de una decisión simple, pero potente. El conjunto de decisiones stump es un simplísimo modelo de aprendizaje.
Algoritmos con esta base pueden obtener usualmente un rendimiento razonable. Además suelen ser eficientes y fáciles de implementar; lo que lo convierte en un algoritmo de aprendizaje base muy popular para aprendizaje ensemble.
Perceptron kernel
Podemos extender la solución stump para obtener el kernel Perceptron. El Perceptron es un muy importante modelo de aprendizaje relacionado con el aprendizaje en redes neuronales. Se ha demostrado que el trabajo con el kernel Perceptron equivale a construir una red neuronal con un número infinito de neuronas. Al igual que el kernel stump, el Perceptron trabaja con una dimensión infinita.
Laplacian kernel
Aplicando sobre el kernel stump, un grupo de transformaciones matemáticas, obtenemos una expresión del kernel stump como árbol infinito, dada la combinación de varias funciones stump, utilizando la expansión de la serie de Taylor, obtenemos un equivalente en la teoría ensemble infinita, del tradicional kernel de base radial, Laplace, expresado mediante la fórmula:
- k(x,x')=exp(-Ɣ||x-x'||1),Ɣ>0.
Exponencial kernel
Igualmente aplicando un grupo de transformaciones similares, a partir del kernel Perceptron obtenemos un equivalente del popular kernel exponencial, expresado como árbol de decisiones, Perceptron infinitas, expresado mediante la fórmula:
- k(x,x')=exp(-Ɣ||x-x'||2),Ɣ>0.
Fuentes
- Brugger, D. “Parallel Support Vector Machines”, Departamento de técnicas de la informática, Universidad de Tϋbingen, Dinamarca.
- Platt J.C., “Fast training of support vector machines using sequential minimal optimization,” In Advances in Kernel Methods.